Foreword

Welcome!

This is the manual of AEON, a tool for long term analysis of Boolean networks. In particular, AEON allows you to define Boolean networks with partially unknown update functions. Then, for such a network, you can compute its asynchronous attractors and explore the state space of these attractors. Finally, you can investigate how the attractor structure changes depending on the unknown parts of the network (attractor bifurcation) as well as which variables are stable, unstable, or switched under different conditions (stability analysis). For all of this, AEON uses efficient symbolic algorithms based on BDDs, which make it possible to handle even networks with 1000 or more variables.

In this document, you can find information on how to use AEON to:

• Create a Boolean network or import it from an existing .sbml or .aeon file.
• Create a partially unknown Boolean network with logical parameters.
• Check that the network is consistent with its regulatory graph.
• Compute asynchronous attractors of a Boolean network.
• Visualize the state space of the computed attractors.
• Construct a bifurcation decision tree: A visual representation of the dependence between network parameters and attractors.
• Perform stability analysis of the attractors for different conditions.

AEON is a constantly evolving academic project. If you have any problem or run into some unexpected behaviour, please contact us at sybila@fi.muni.cz. We will be happy to help you and make AEON a more useful tool for you. Finally, if you found AEON useful in your research, please cite it using the following publication:

Beneš, N., Brim, L., Kadlecaj, J., Pastva, S., & Šafránek, D. (2020, July). 
AEON: Attractor Bifurcation Analysis of Parametrised Boolean Networks. 
In International Conference on Computer Aided Verification (pp. 569-581).

Introduction

AEON is available as an online tool at https://biodivine.fi.muni.cz/aeon/. On this website, you can pick the version of AEON you want to use (naturally, we recommend the latest version), and you will be redirected to its online interface, which should look similar to this:

AEON User interface.

In the middle, there is a quick help message, which disappears when you load a Boolean network, but you can always bring it back by holding down H. On the left, there is a main menu which you can use to import existing networks, manage the details of your model, or start attractor analysis.

If you for whatever reason cannot access this website, there is a mirror on Github pages, but the version there may not be always up to date. Alternatively, you can also run your own instance of AEON. It is a simple static HTML/JavaScript website, and the sources are available on Github. See the Building AEON chapter for more details.

Out of the box, AEON allows you to perform basic actions, like creating or editing a Boolean network. However, AEON uses a native compute engine which handles computationally intensive tasks efficiently outside your browser. Therefore, to do almost anything beside editing Boolean networks, you need a compute engine the website can connect to. In the next chapter, we discuss how to download and run this compute engine.

At the moment, due to security reasons, some browsers are blocking non-HTTPS JavaScript connections to foreign websites if the page itself is using HTTPS. For this reason, you may not be able to connect to a local compute engine from Safari, Brave or other browser with this policy. If you can, please use Chrome for the rest of this tutorial.

AEON Compute Engine

To download the compute engine for the version of AEON you are using, pick Compute Engine in the left menu, and download a pre-compiled binary for your operating system. Compute engine binaries for different versions of AEON are in general not compatible, and you should be therefore always using the compute engine of your current version:

Downloading AEON compute engine.

Once the download is finished, you can unzip the file. Inside, you should find a compute-engine binary that you need to execute.

The binary is not signed for distribution on MacOS, so you may need to add a security exception if you want to run it on a Mac.

When you execute the binary, you should see a terminal window with an output similar to this:

🔧 Configured for production.
    => address: localhost
    => port: 8000
    => log: critical
    => workers: 8
    => secret key: generated
    => limits: forms = 32KiB
    => keep-alive: 5s
    => read timeout: 5s
    => write timeout: 5s
    => tls: disabled
Warning: environment is 'production', but no `secret_key` is configured
🚀 Rocket has launched from http://localhost:8000

The compute engine automatically starts a local webserver on port 8000 through which it communicates with the AEON website. You can set the environmental variable AEON_PORT to whatever you need the port to be.

If you can't for any reason run the binary (for example, some Linux systems seem to have problems with outdated glibc), you can build it from source. Instructions for this are quite simple, and you can find them in the Building AEON chapter.

Once compute engine is running, you can go back to the AEON website and either (a) refresh the website, if running correctly, the compute engine should connect automatically, or (b) press Connect in the Compute Engine panel to manually retry the connection. You should see the status change from disconnected to connected, and the dot next to the Compute Engine should change its color to green.

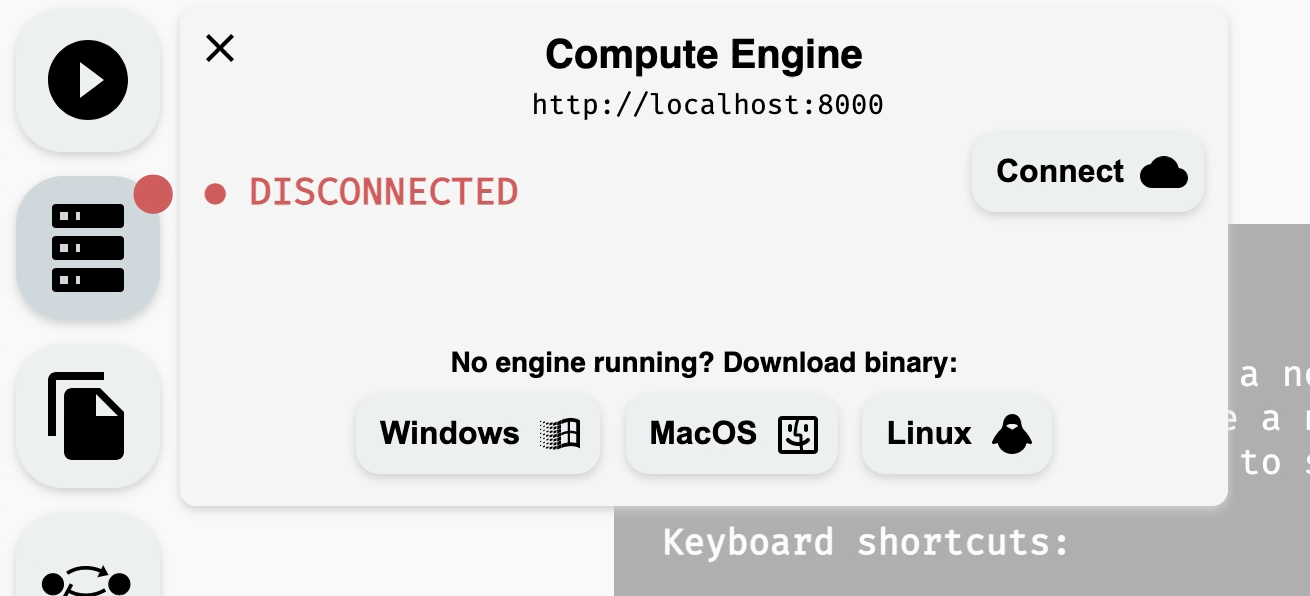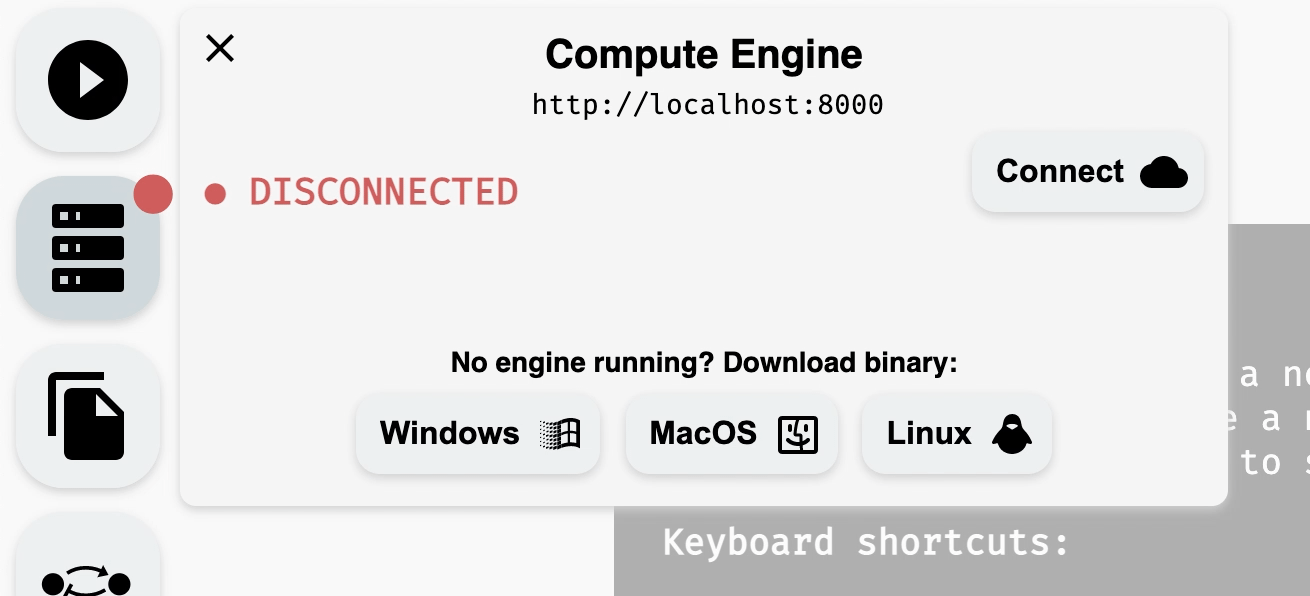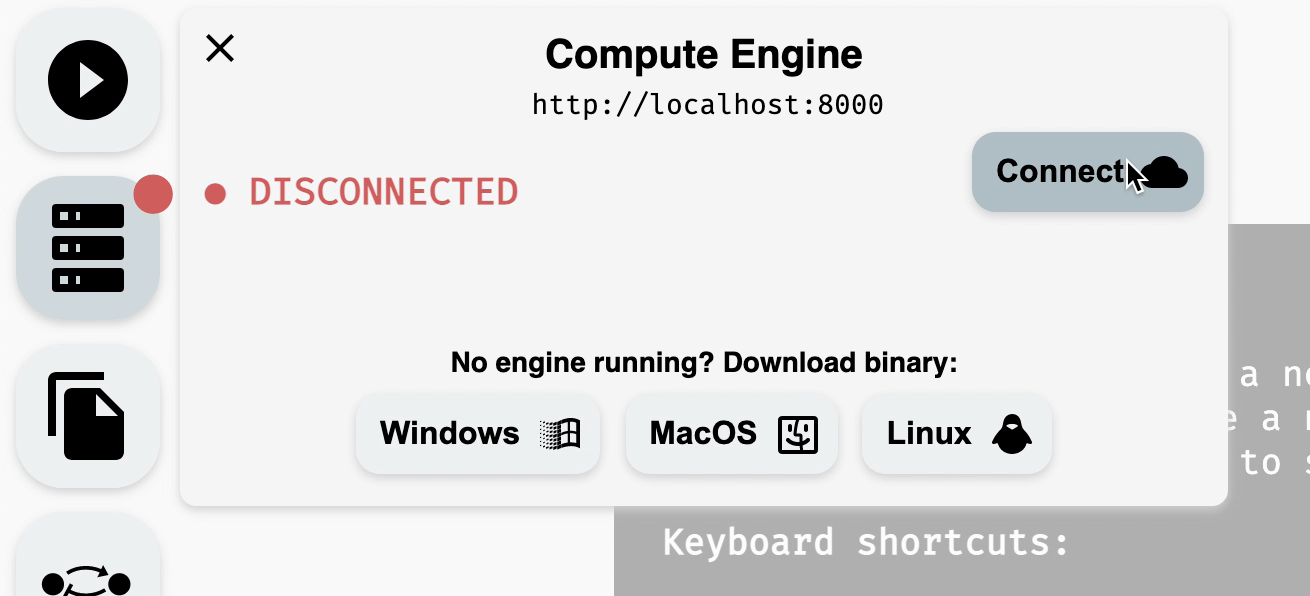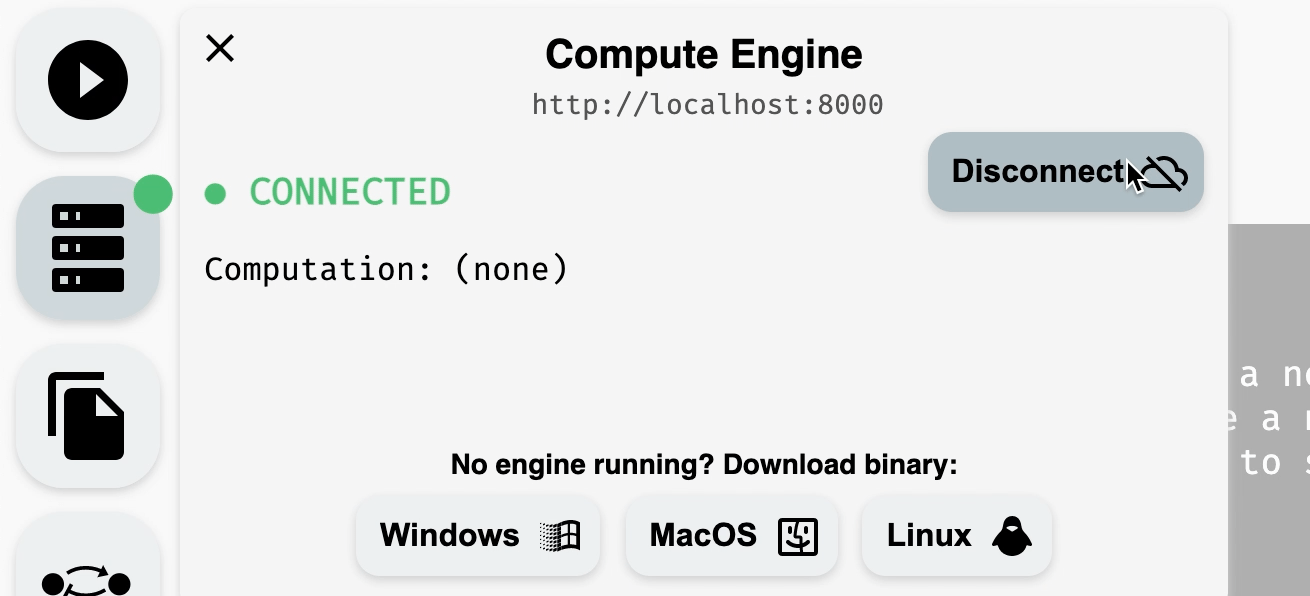Connecting to a running compute engine.

If you changed the AEON_PORT value, you need to also update the engine address in the Compute Engine panel — click the default address http://localhost:8000 to edit it.

WARNING: At the moment, the compute engine supports only one active session of AEON at a time (this will be resolved in future versions of AEON). If you have multiple tabs with AEON open, and they all connect to the same compute engine, they can see and override each other's data! You can still use multiple tabs to edit or view networks, but keep in mind that analysis results (attractors and bifurcation decision trees) are available only for the last computed tab.

Now, you should be ready to use all features available in AEON.

Model Editor

In this chapter, we discuss how to create, import, modify, and export Boolean networks, as well as how to enhance them with logical parameters. If you only want to work with existing Boolean networks (available as .sbml or .aeon file), i.e. you are not planning to edit the network, just import it, you can skip to the last section of this chapter.

AEON model editing functionality is distributed between two main editor "components": an interactive regulatory graph editor, and a model panel. The regulatory graph editor is the main area of the AEON window, while the model editor can be opened by clicking the Model Editor button in the left menu.

Model panel (left) and regulatory graph editor (right)

We first focus on the regulatory graph editor, and show how to manipulate network variables and regulations. Then, we shift our focus to the model panel and show how to edit network update functions or add parameters. Finally, we look at structural properties of regulatory graphs and how AEON verifies these properties on-the-fly. At the end of the chapter, we discuss model formats supported by AEON.

Variables and regulations

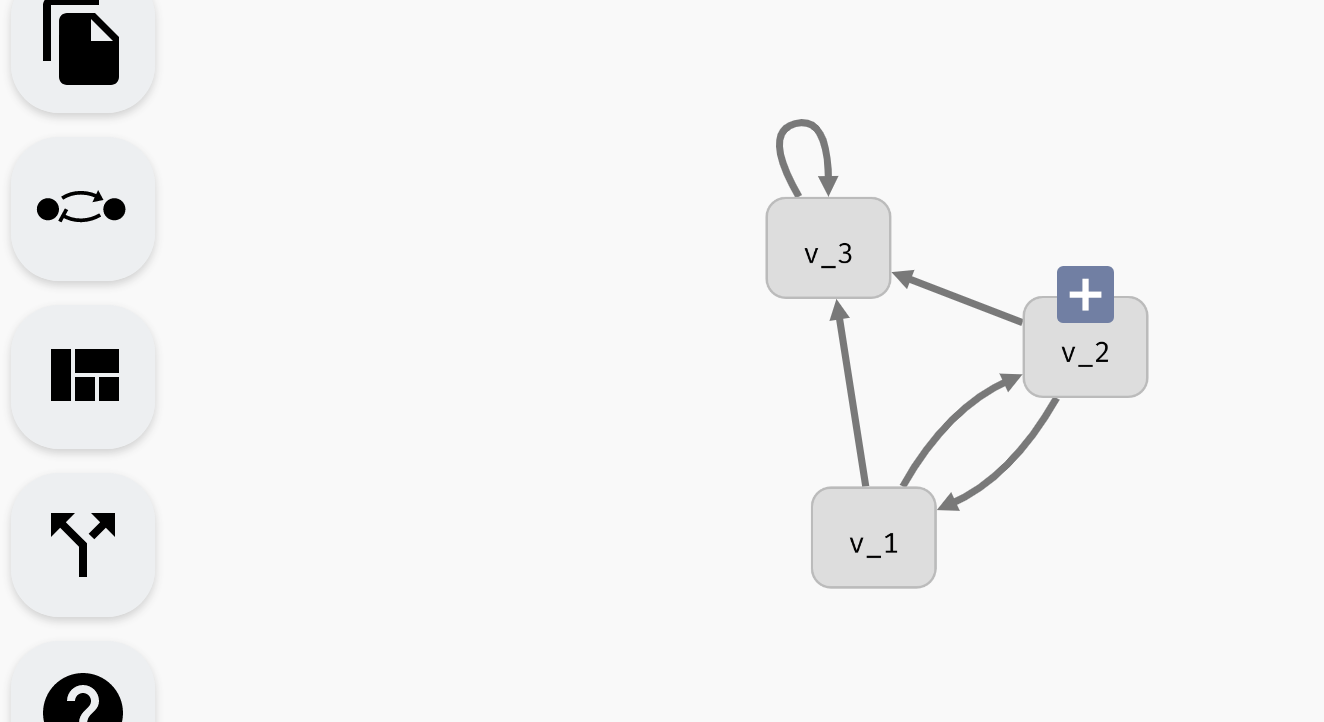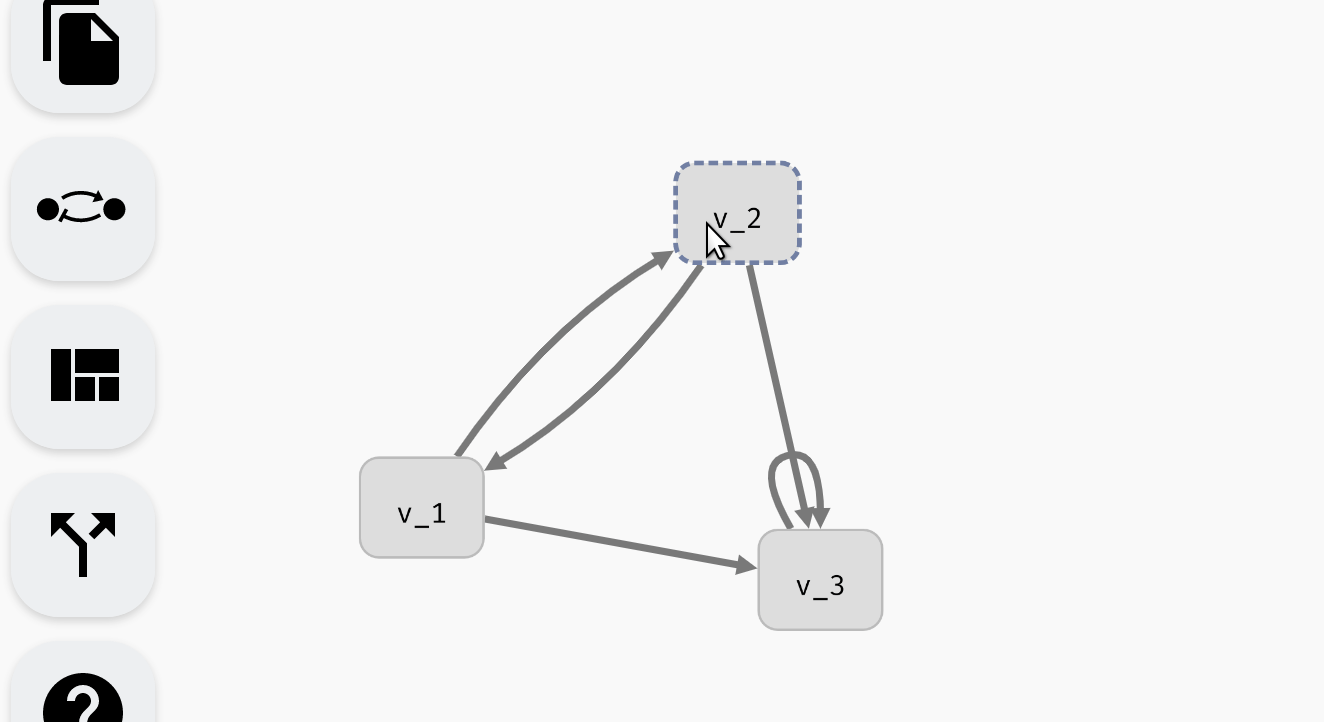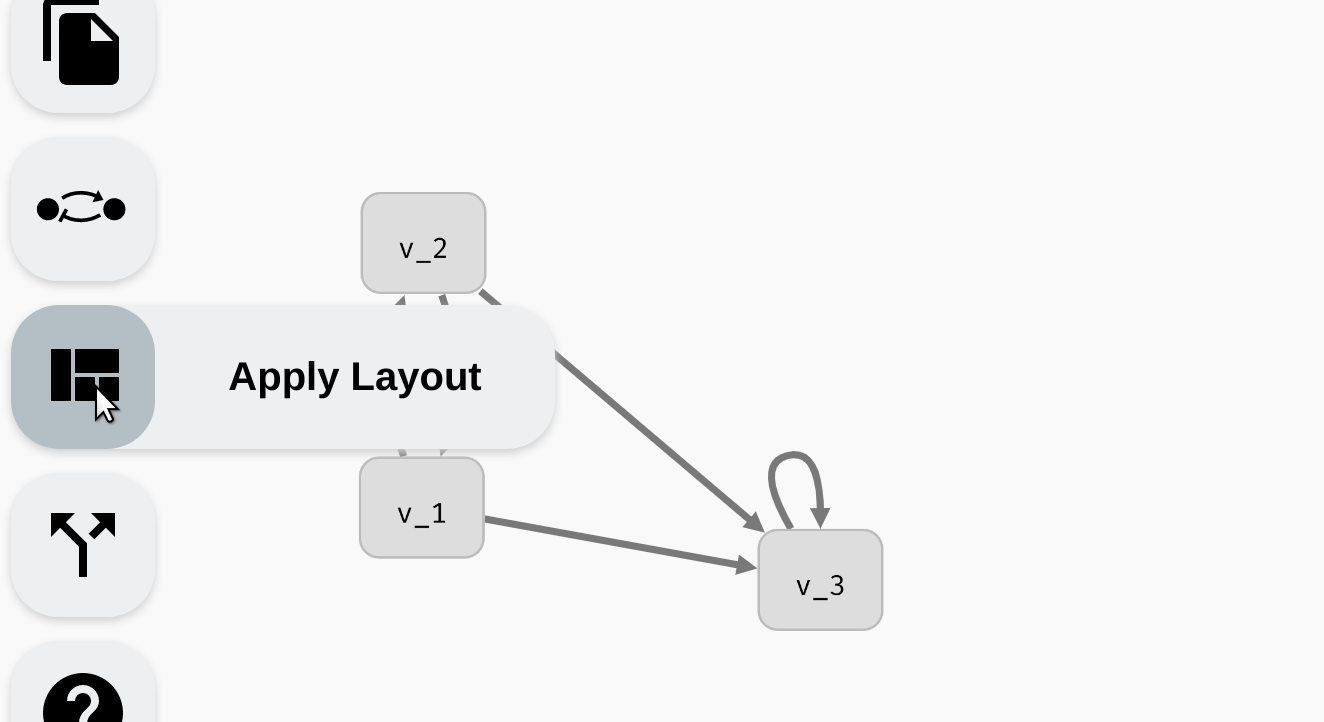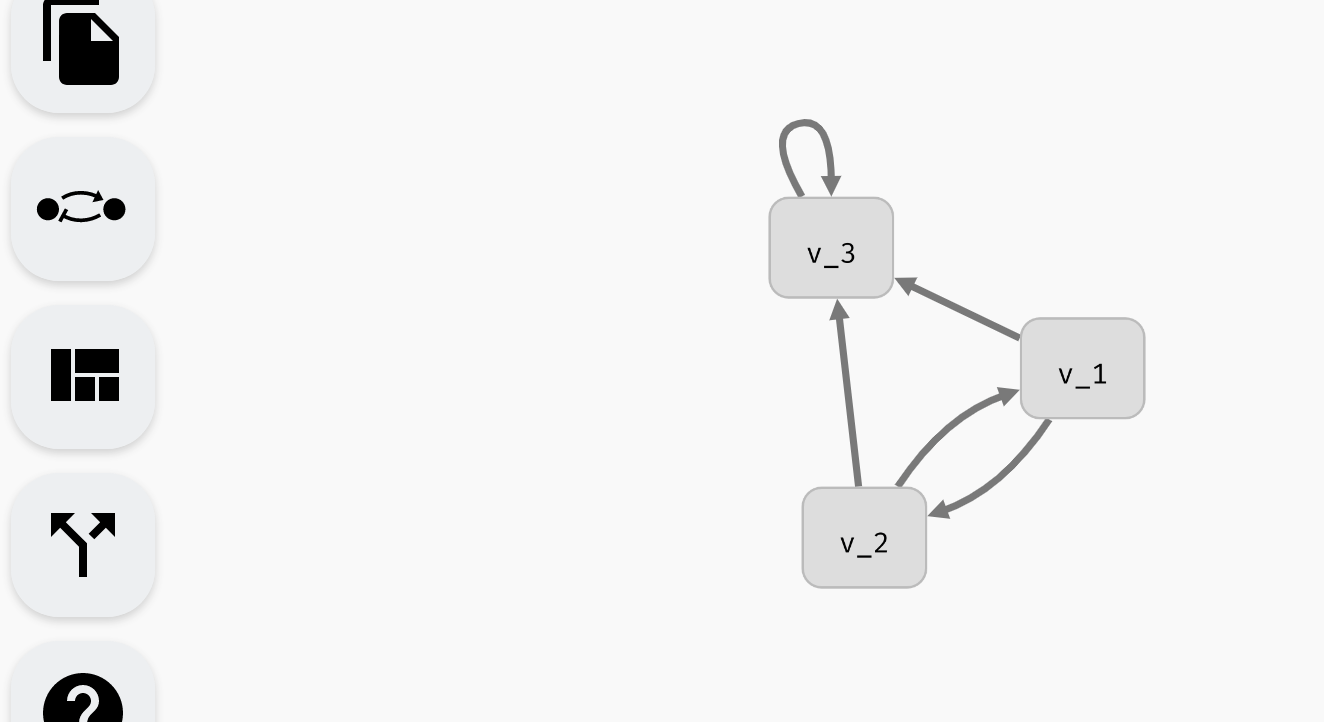
To create a new variable, double-click anywhere in the empty space of the AEON window. A new variable node will appear at that location (You can also press N to create a new variable node at a default location). A variable node in a regulatory graph represents one variable of a Boolean network. When you move the cursor over this variable node, a blue + icon appears. By dragging from this icon to some variable node, you can create regulations, i.e. edges of the regulatory graph. Note that self-loops (auto-regulations) are also supported. A regulation edge from A to B represents a (possible) dependence of B on A.

Creating variables and regulations in the regulatory graph.

You can click and drag variable nodes to re-arrange them however you like. To help with arranging large networks, AEON contains an auto-layout algorithm that you can activate using the Apply Layout button in the left menu.

Auto-layout functionality.

Finally, each variable node or regulation edge can be selected by clicking. This opens a variable or regulation menu. Through here, you can access additional options, such as removing a variable or regulation (which you can do using backspace as well). You can also rename a variable, which opens the model panel and focuses the edit field of the variable name. We will talk about the remaining options in edge and regulation menus in the following sections.

Deleting and editing regulatory graph elements.

Model panel and update functions

Once the regulatory graph of your Boolean network is in place, you can assign each variable an update function. The update function of variable A takes the values of its regulators (sources of the regulation edges terminating in A) and computes a new value of A based on these values.

For example, consider the following regulatory graph:

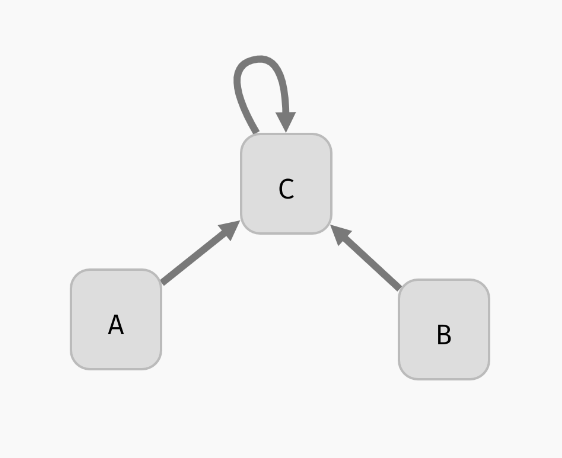
Here, variable C is regulated by every variable. That is, update function of C should depend on A, B, and C. For example, we can open the model panel and set the update function to C | (!A & !B). This will make C true if it already is true, or if both A and B are false.

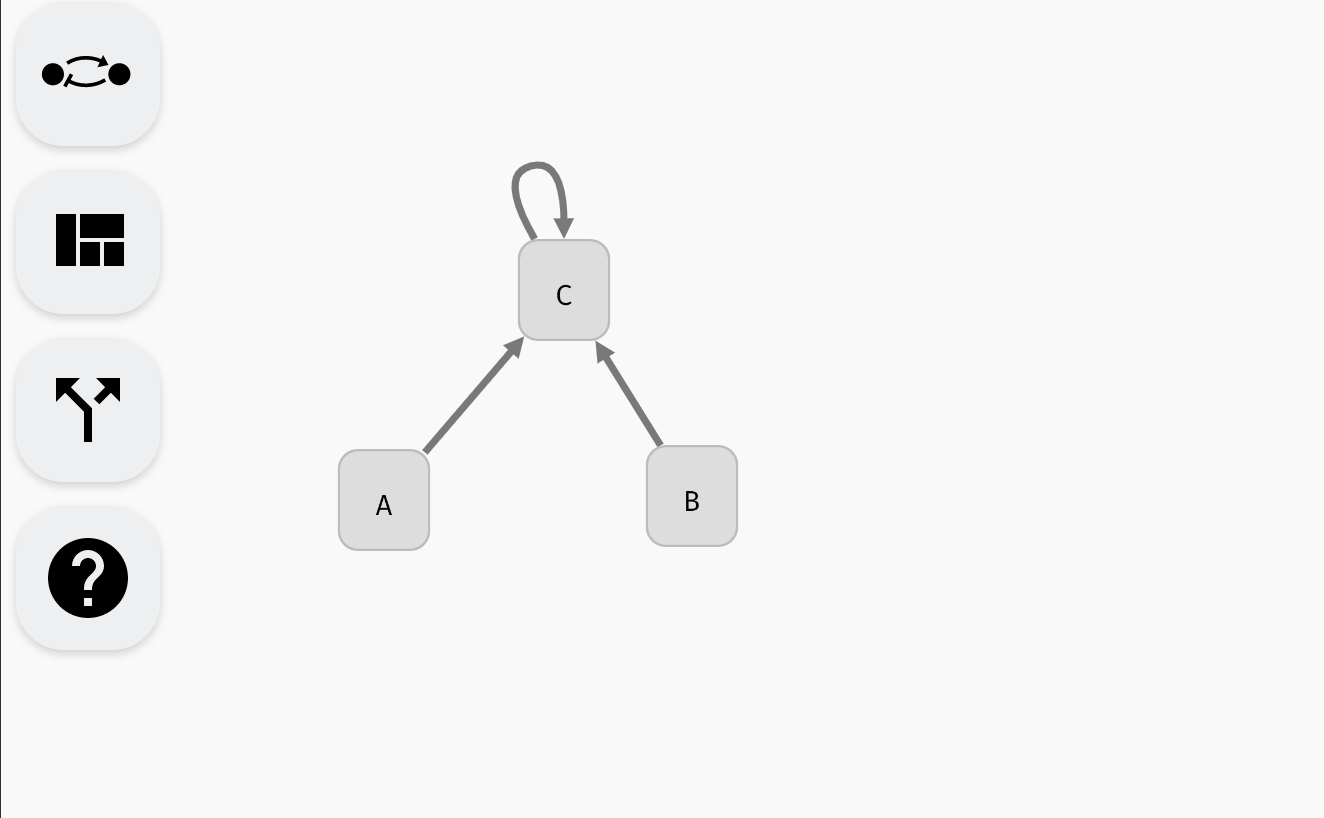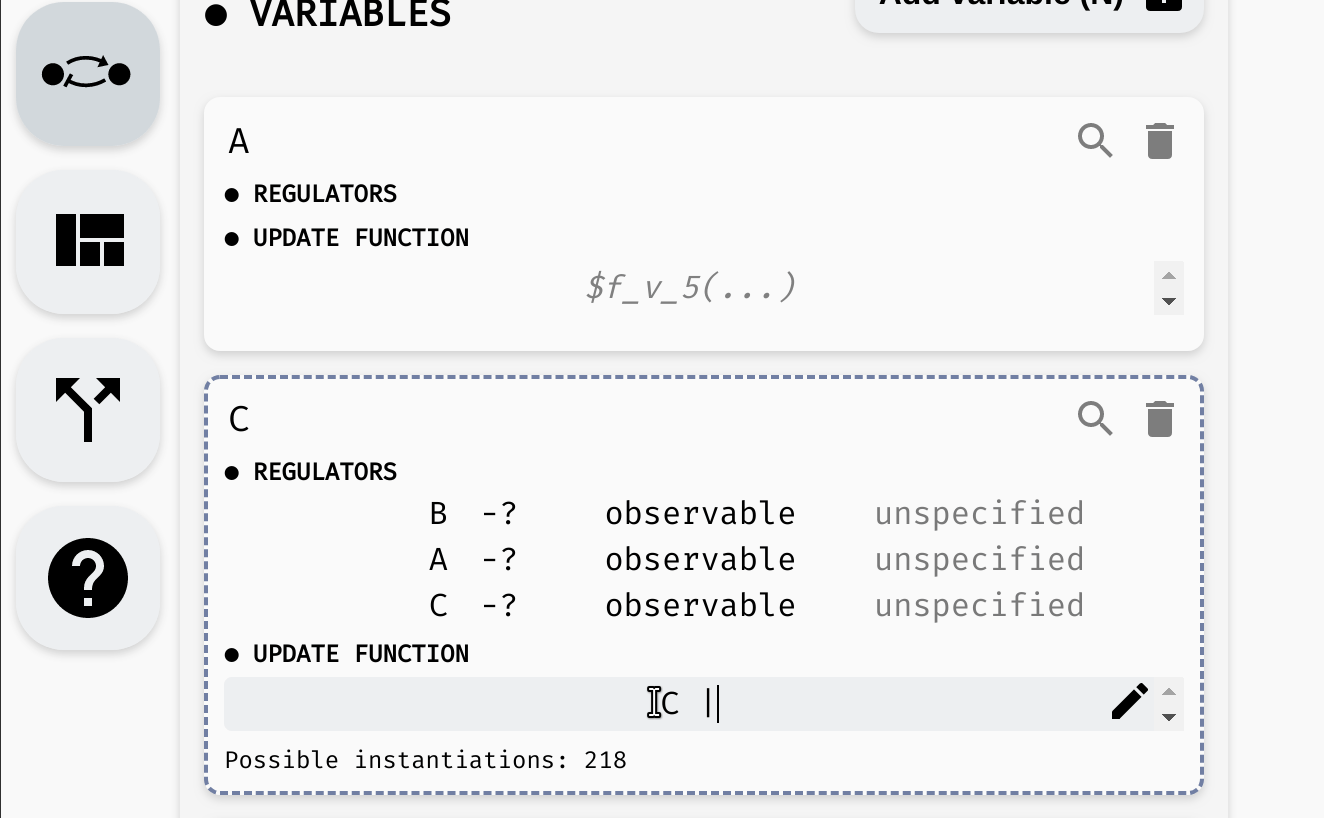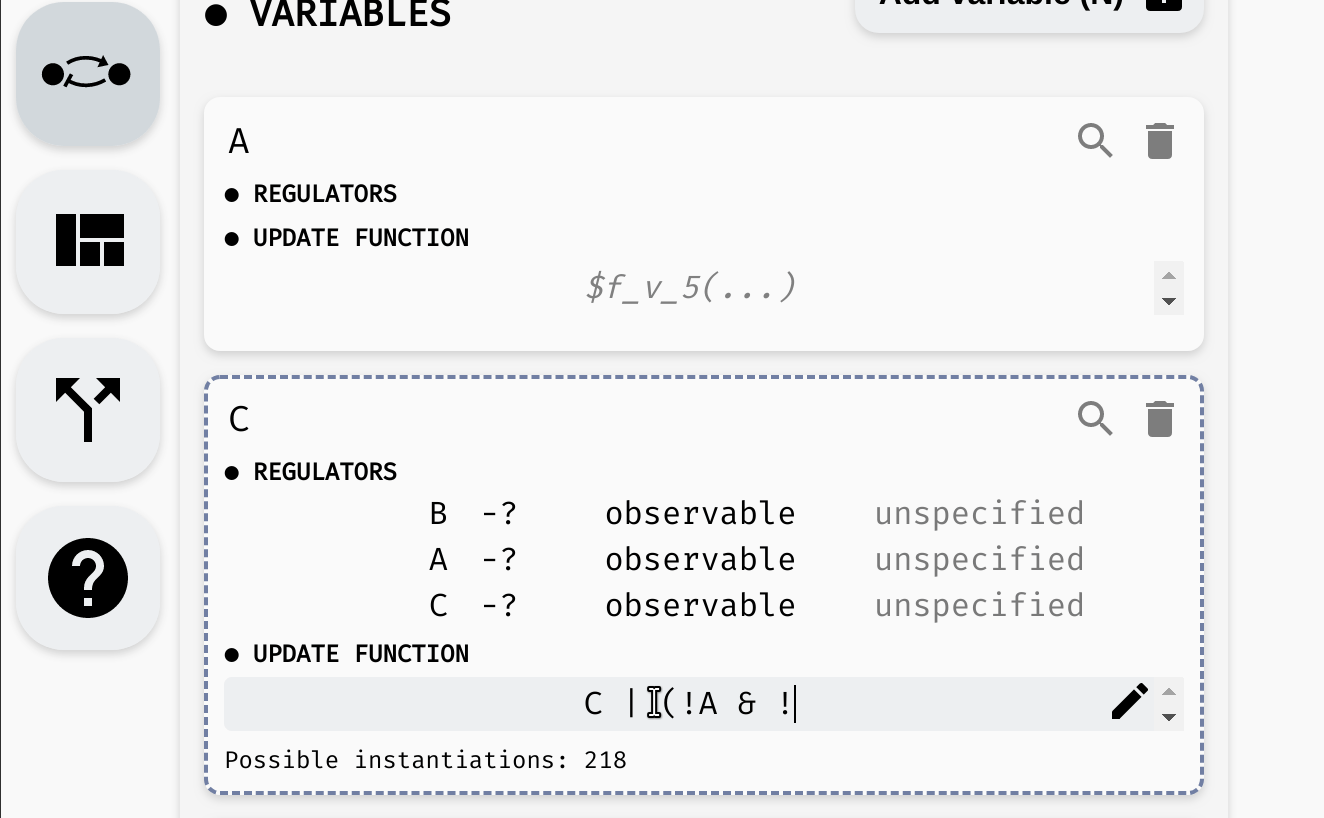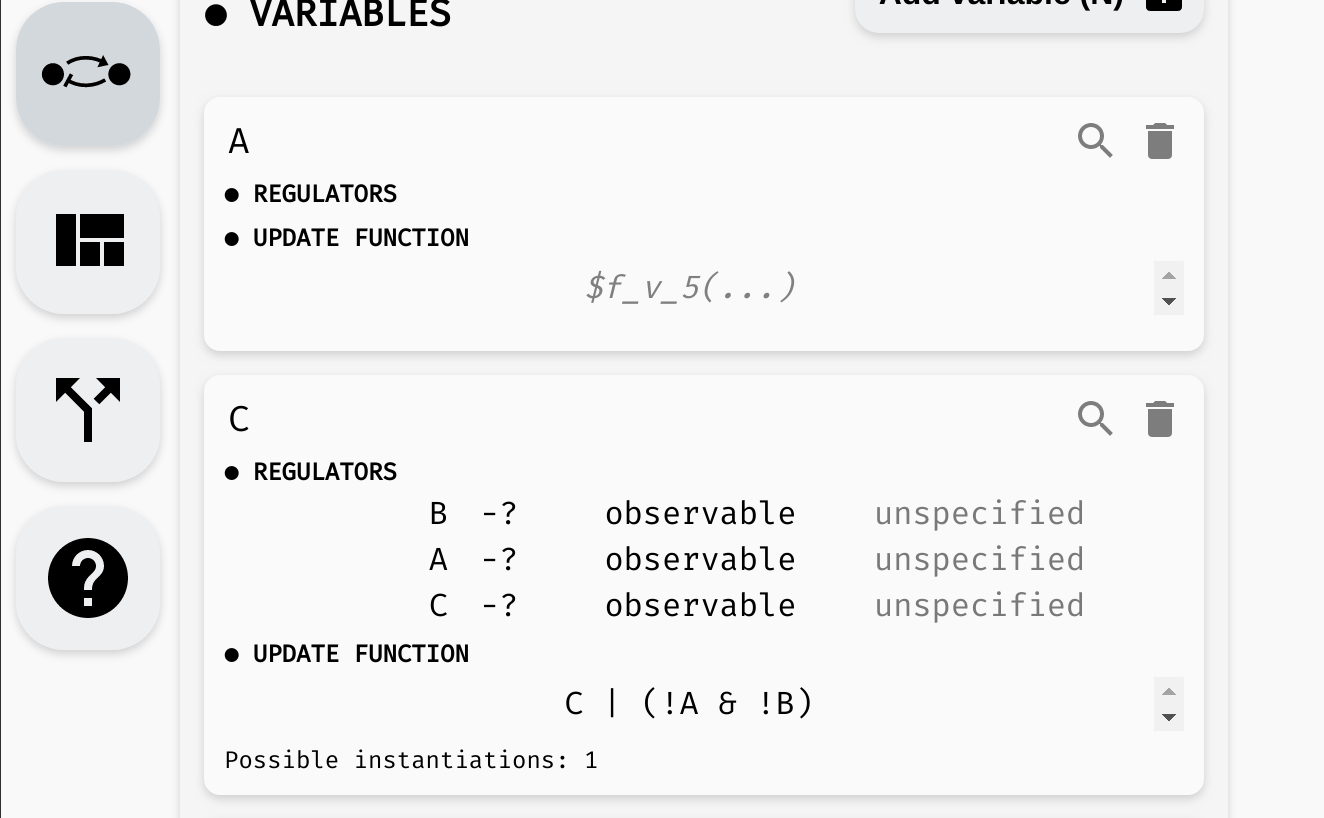Setting the update function of C.

The behaviour of the Boolean network is described using a state transition graph, where the graph vertices are the states of the network (each state assigns true or false to every network variable), and the edges correspond to applications of individual update functions to the network states. In our network, a state A=false, B=false, C=false can transition into A=false, B=false, C=true by updating the variable C.

Note that A and B have no regulations, therefore their update functions do not depend on any variable and must be constant: true or false. In general, an update function can use the constant values true/false, names of the regulating variables, parenthesis (), and (&), or (|), implies (=>), if and only if (<=>) as well as xor (^). You can add new-lines and arbitrary whitespace to the update function, but AEON will not save this information to the exported model file.

Other model panel functionality

Aside from setting the update functions, in the model panel, you can create/remove variables as well as edit their names (as we have already seen). In a large model, it can be also useful to locate a specific variable in the regulatory graph using the magnifying glass button.

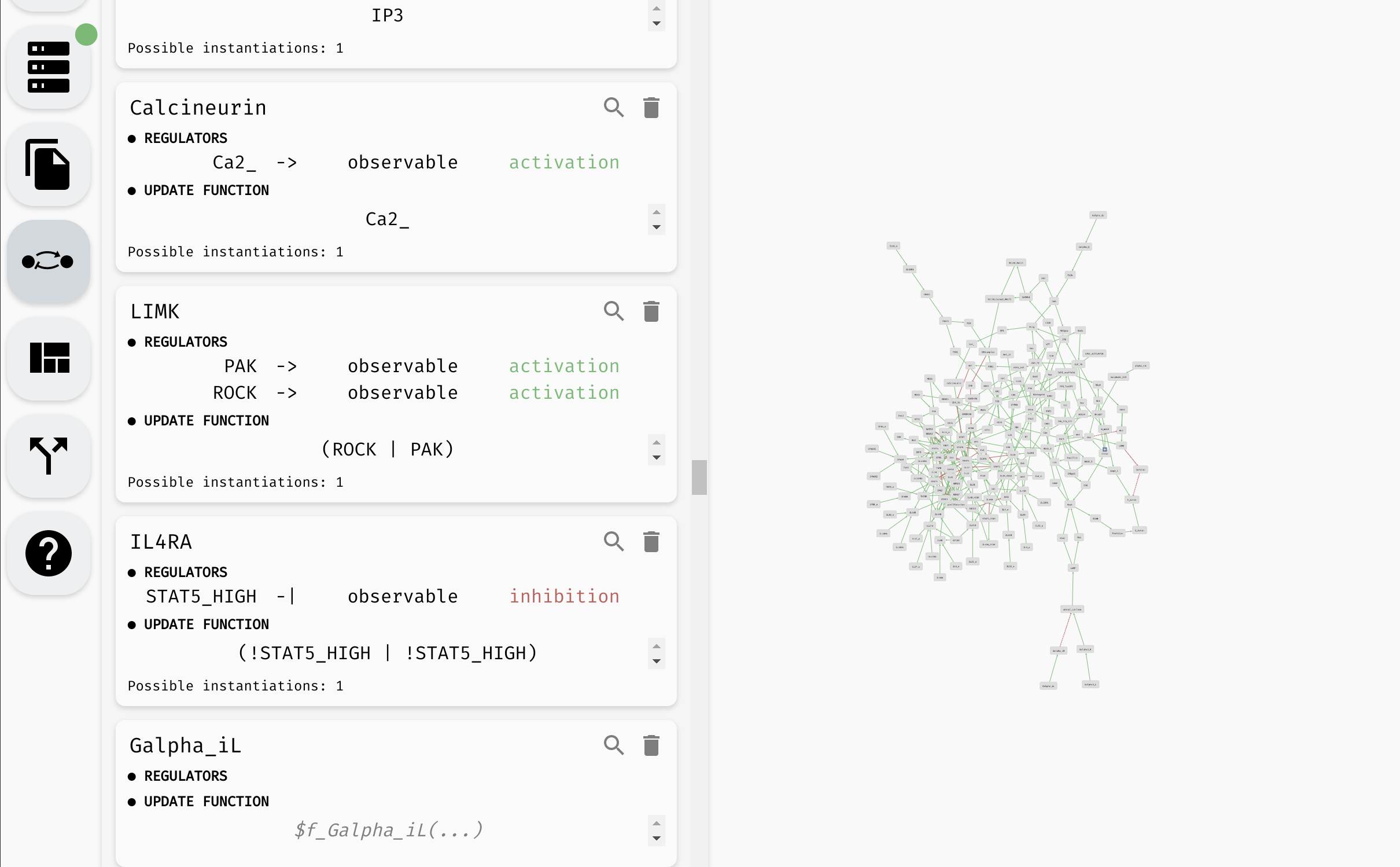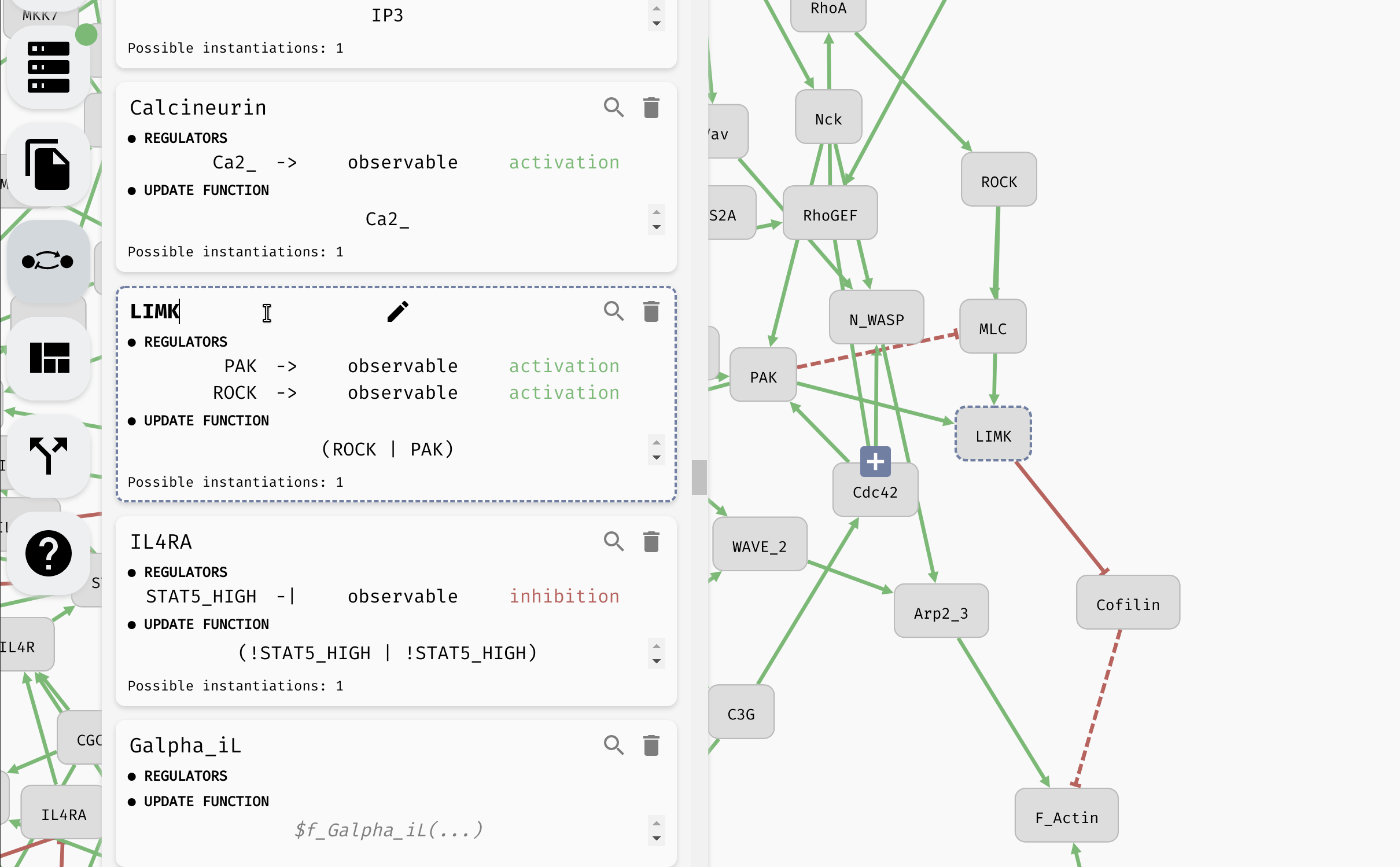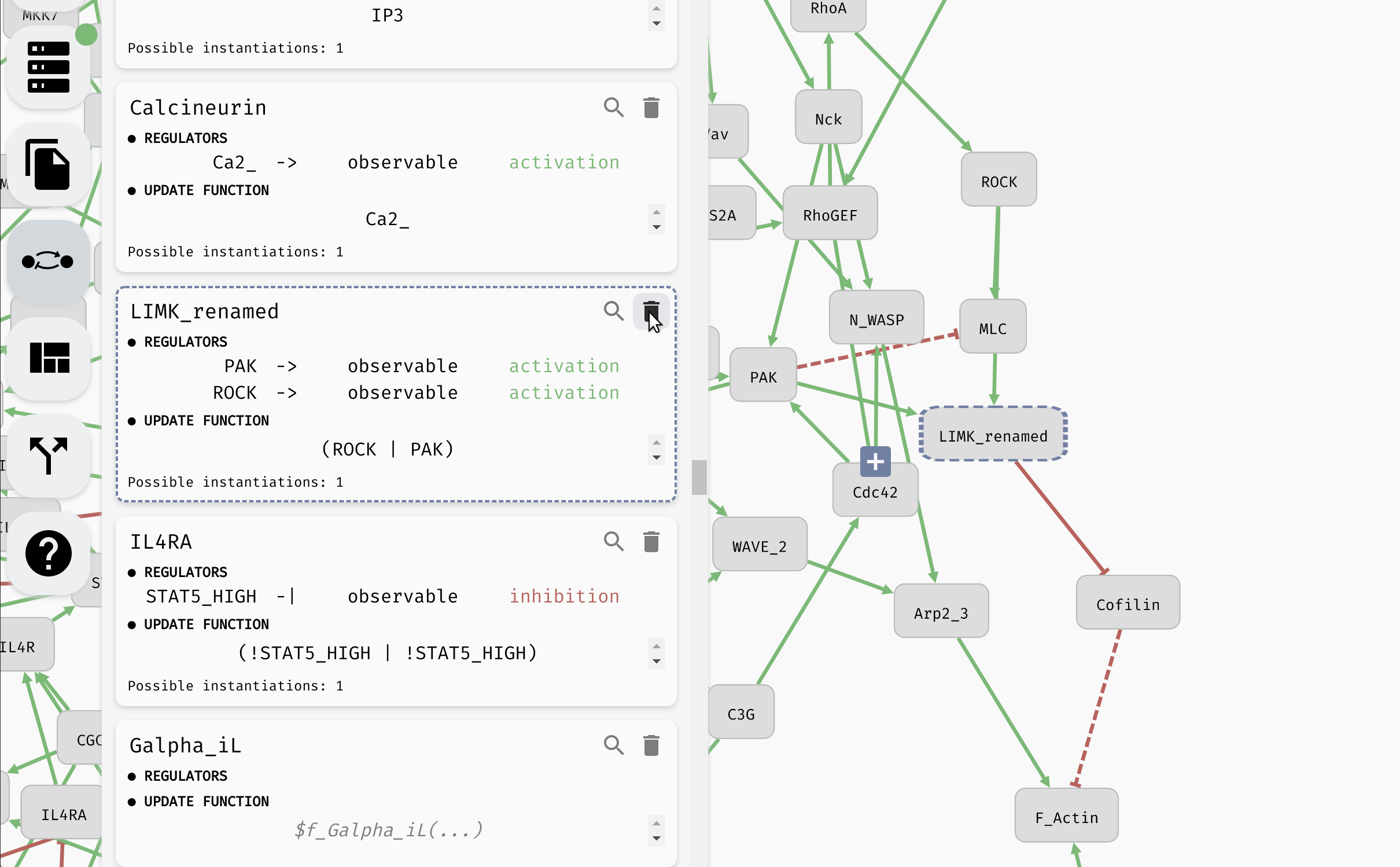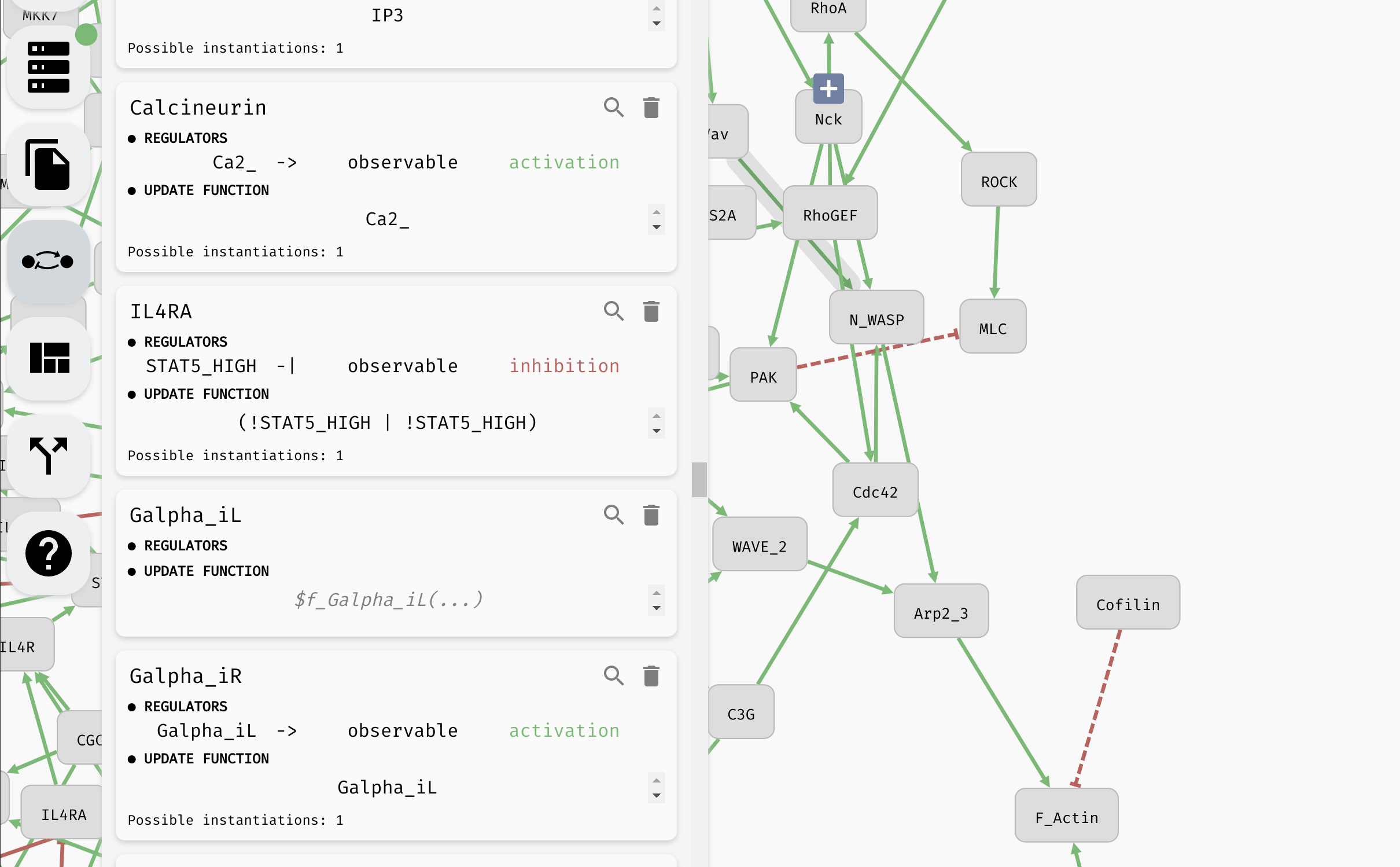Looking up and editing a variable in a model panel.

Hint: When the model is very large, you can use the "Find..." feature of your browser to look for specific variables in the model panel.

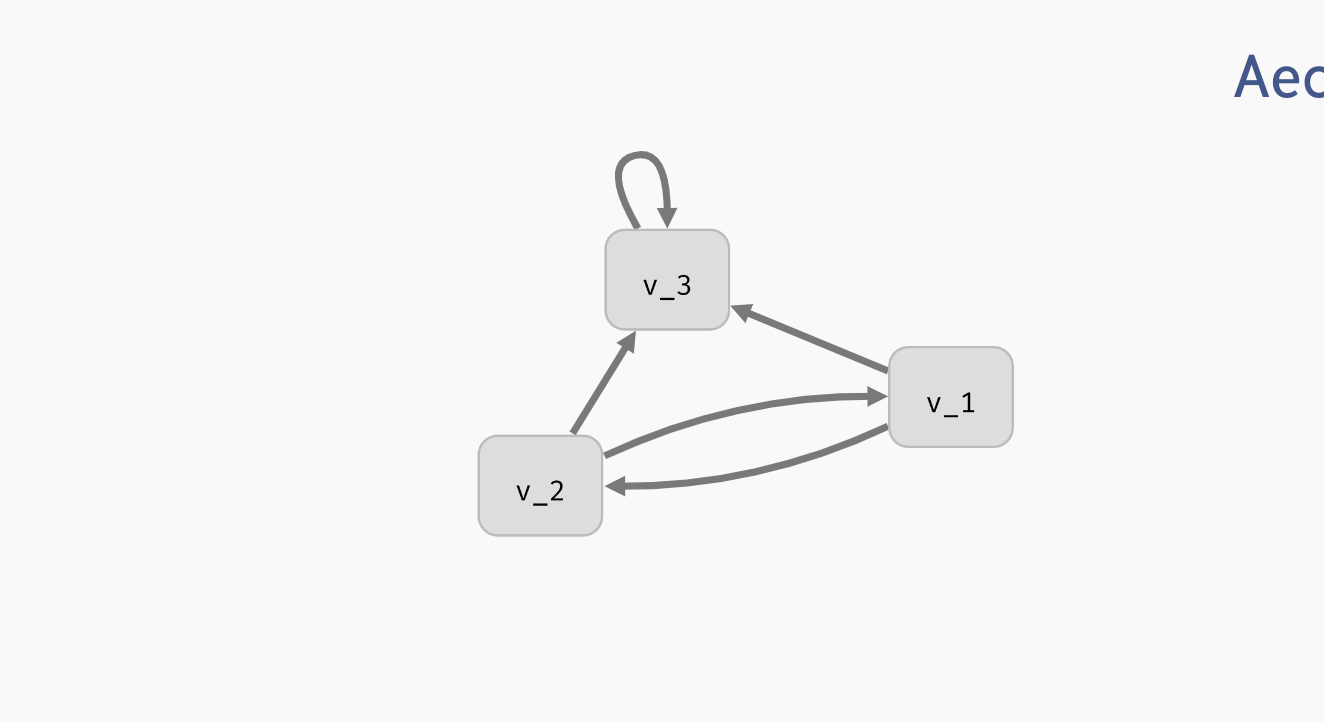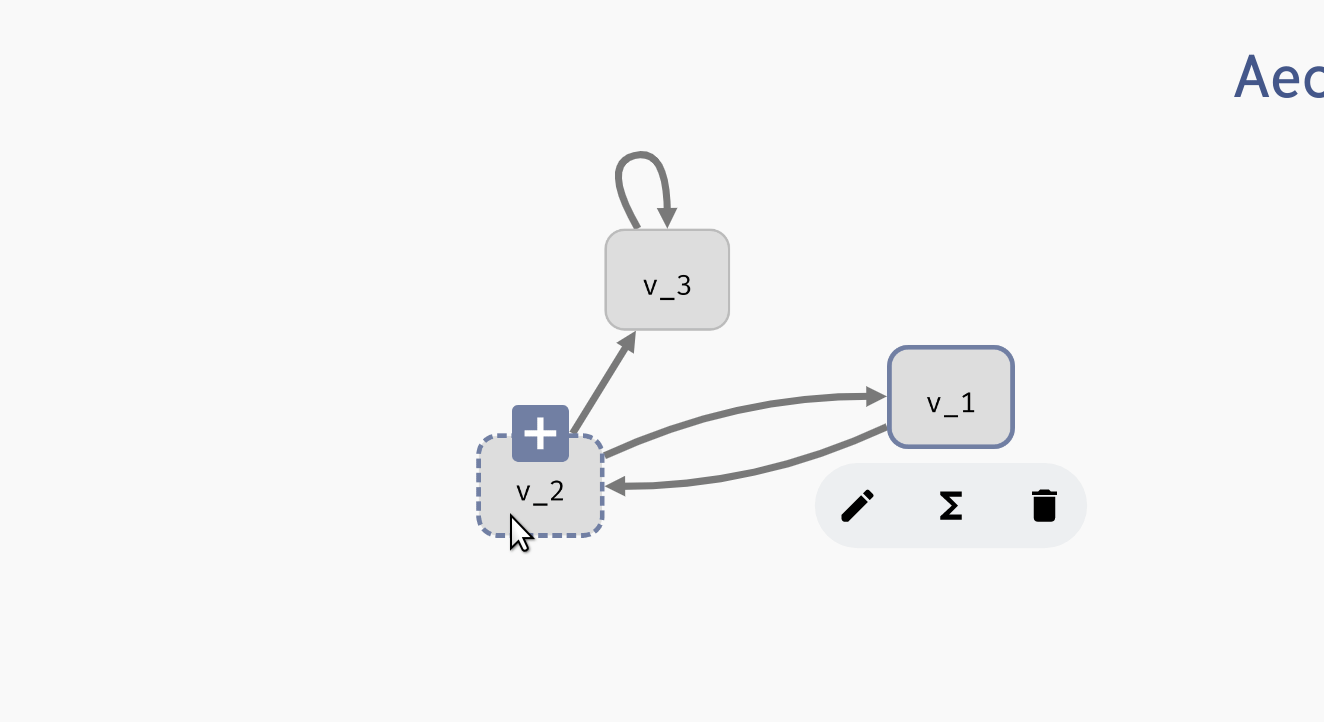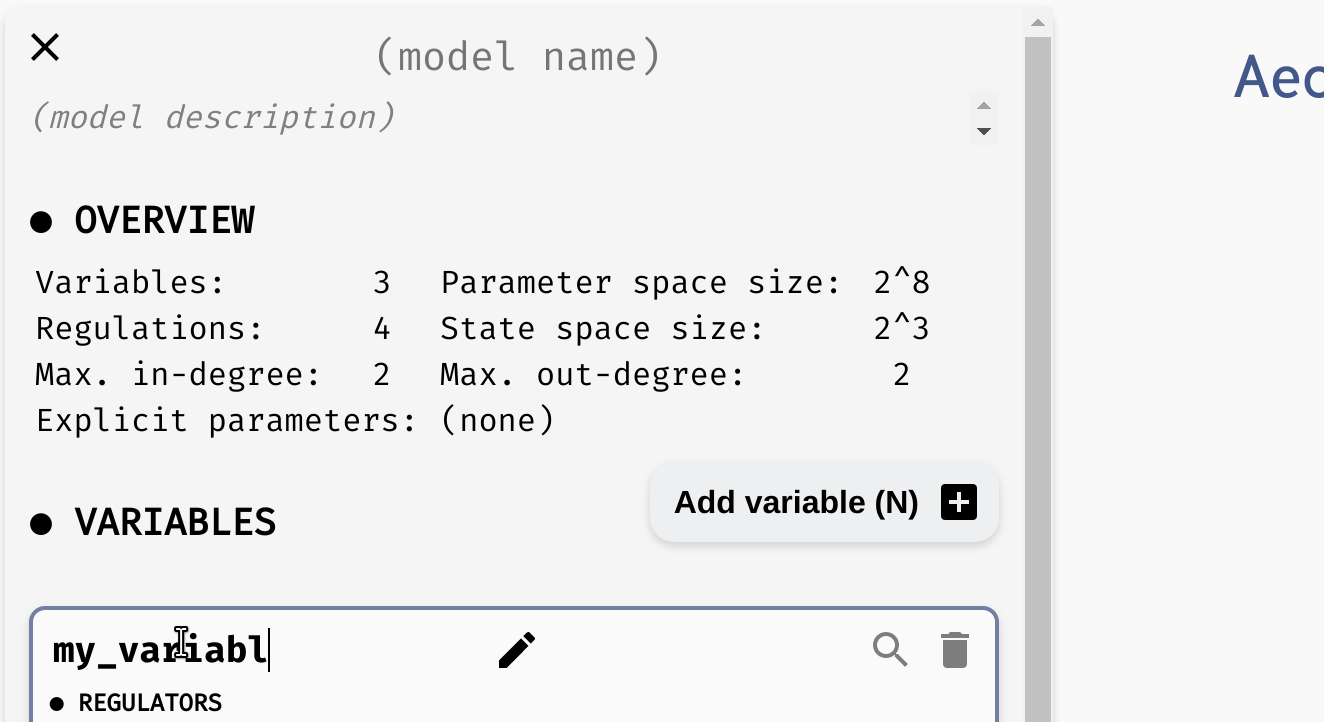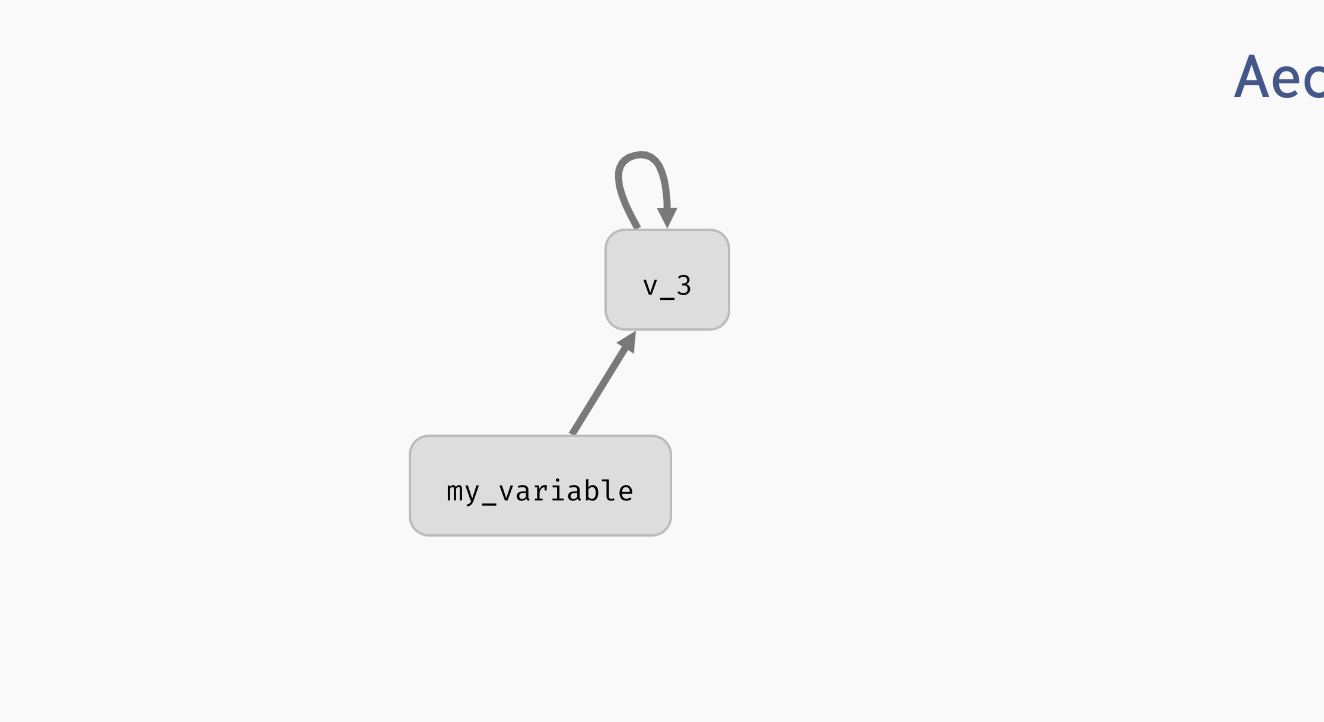
Finally, at the very top of the model panel, you can find an edit field where you specify the name of your model, as well as some general description of the model. This part of the panel also contains a general overview of the model, including:

• Number of Boolean variables and regulations between them.
• Maximal in-degree and out-degree (number of incoming and outgoing regulations) in the model.
• Size of the models state space.
• Size of the parameter space, as well as names of the logical parameters.

The name, description, and overview of a particular model.

Parametrised networks

In practice, we often don't know the exact update functions that govern the behaviour of the network. In AEON, you can therefore analyse even a network that is partially unknown. In such case, we say that the network has logical parameters. These parameters can be of two types:

• We say that a variable is implicitly parametrised when its entire update function is unknown. For example, in the model from the previous section, since we did not set any update function for A or B, they are both implicitly parametrised.
• An update function is explicitly parametrised when it contains unknown Boolean expressions. These are expressed using uninterpreted functions. For example, in the model from the previous section, we could set the update function of C to be C | f(A, B). Here, f is an explicit parameter: an uninterpreted function of arity 2. This way, we are giving a partial specification of the update function: we know that when C=true, the value of the function is also true. However, if C=false, we know the result depends on A and B, but we don't know what that dependence looks like.

An uninterpreted function of arity zero can be also used without argument parenthesis, in which case it resembles a more traditional logical parameter. For example, we can write (K => A) & (!K => B) where A and B are variables, but K is an explicit parameter.

At the moment AEON only allows variables as arguments of uninterpreted functions. That is, you cannot use complex expressions such as C | f(A & B, C). This restriction may be lifted in the future.

In AEON, we then consider all possible instantiations of these logical parameters. That is, AEON considers every possible Boolean function that can be substituted in place of either the explicit or implicit uninterpreted functions.

Note that the number of such functions grows very quickly (there are 2^(2^n) Boolean functions with n arguments). For this reason, AEON typically cannot handle uninterpreted functions (explicit or implicit) with more than 5 arguments (which corresponds to 2^32 possible functions).

In the user interface, you can see this in the form of Possible instantiations: ... label under each update function input field. If the function is fully specified (no parameters), there should be one instantiation: the function itself. As soon as parameters are introduced (or the function is removed completely), the number of instantiations should grow.

For example, update functions for variables A and B from our example should have two instantiations (true and false), while the C | f(A, B) function will have 10 instantiations, as there are 10 binary Boolean functions that depend on both inputs (There are 16 binary Boolean functions, but 6 of them, true, false, A, !A, B, and !B do not depend on both inputs).

Parameters will come into play later, when we discuss the long term behaviour of Boolean networks. Now, lets look at how we can reduce the number of possible instantiations of a parametrised network by enhancing the regulatory graph with additional structural properties.

Regulatory graph properties

In our regulatory graphs, to this point, we assumed each regulation should have some effect on the output of the update function. This is a fairly reasonable assumption (if the regulation has no effect, it has no reason to be in the graph). However, we often have some additional information about the nature of the regulation.

Regulation monotonicity

Many biological processes are either positively or negatively monotonous. In such case, we can mark a regulation as activation (positive monotonicity), or inhibition (negative monotonicity). To do this, you can either use the corresponding button in the regulation menu, or toggle the regulation status in the model panel.

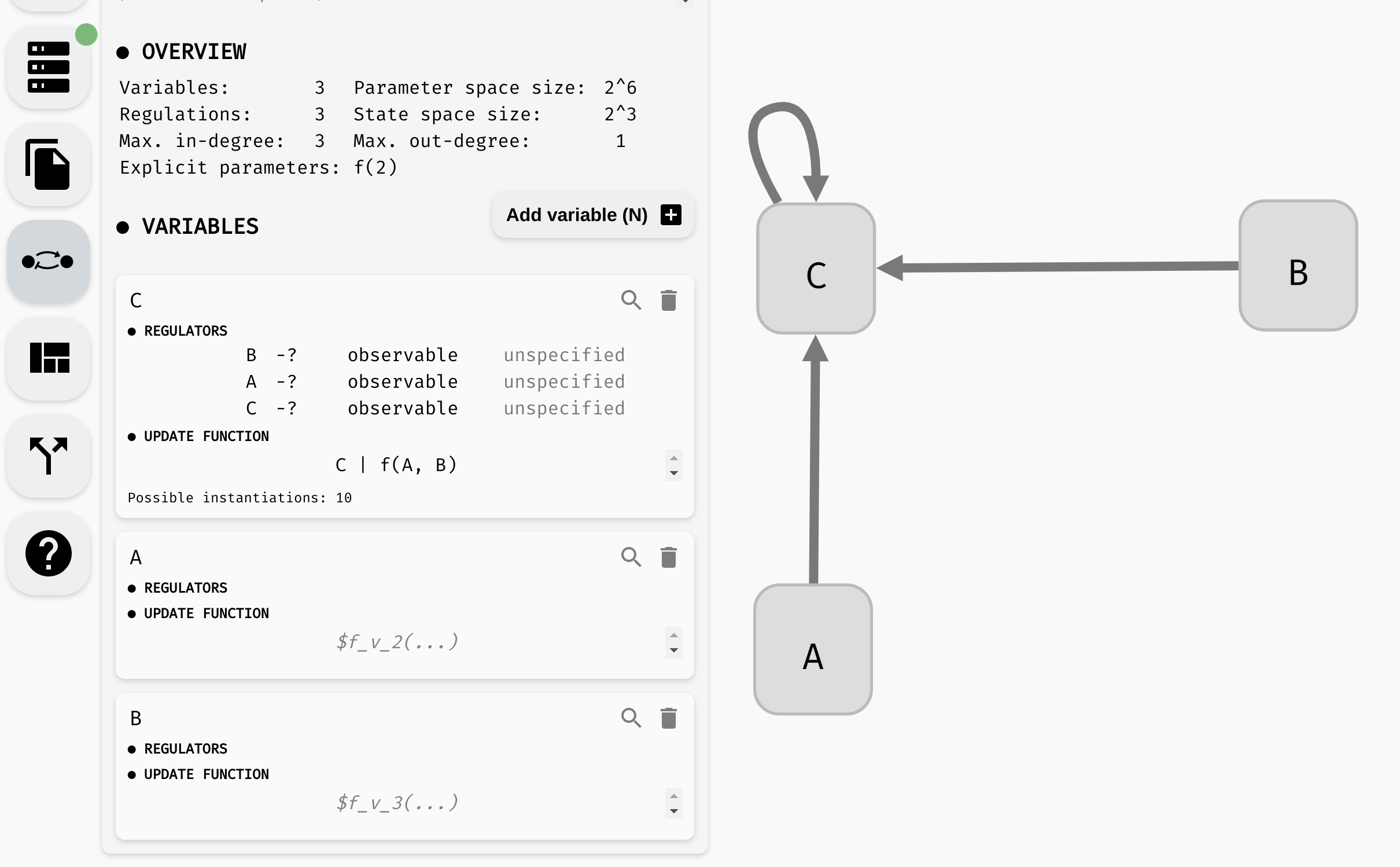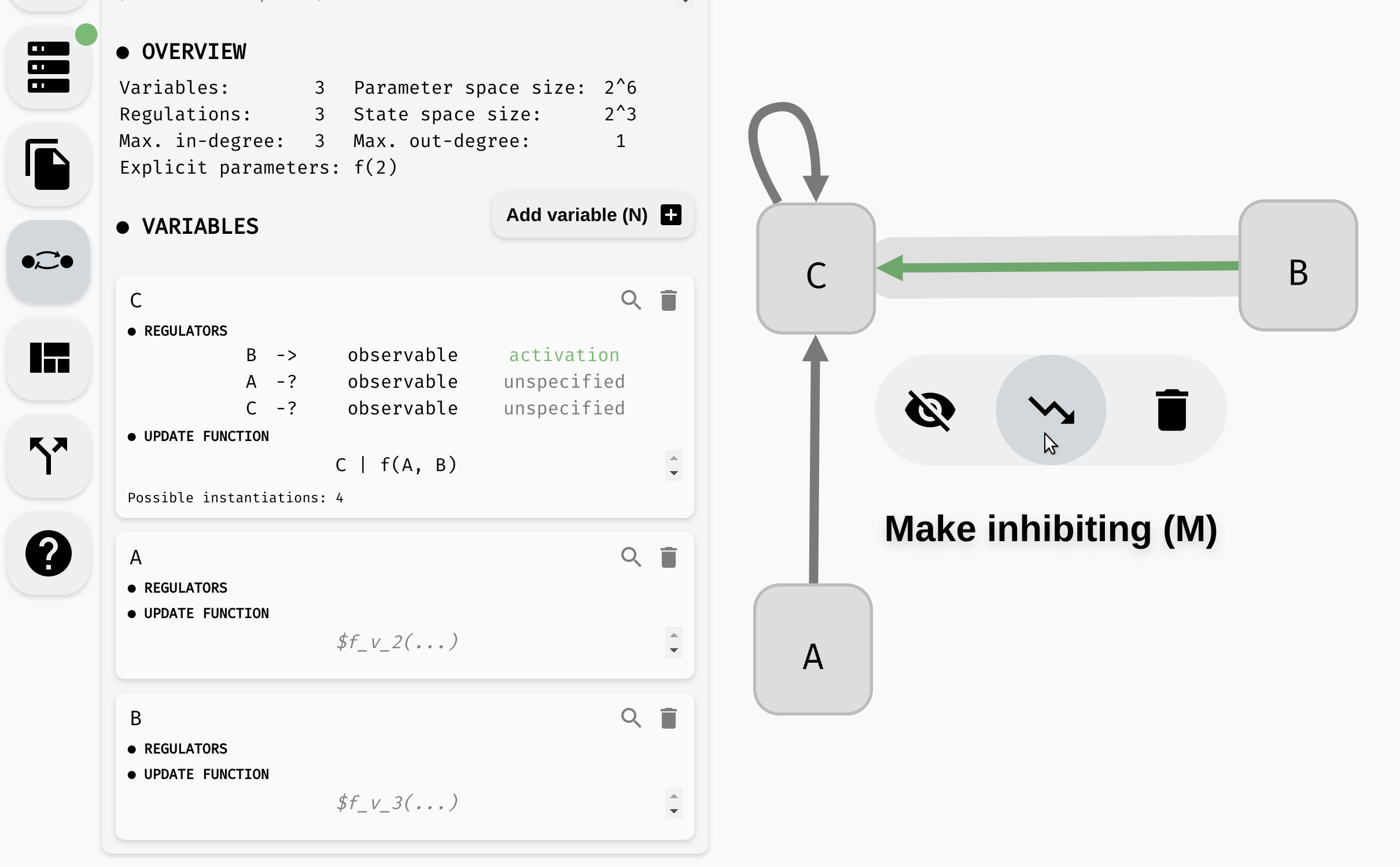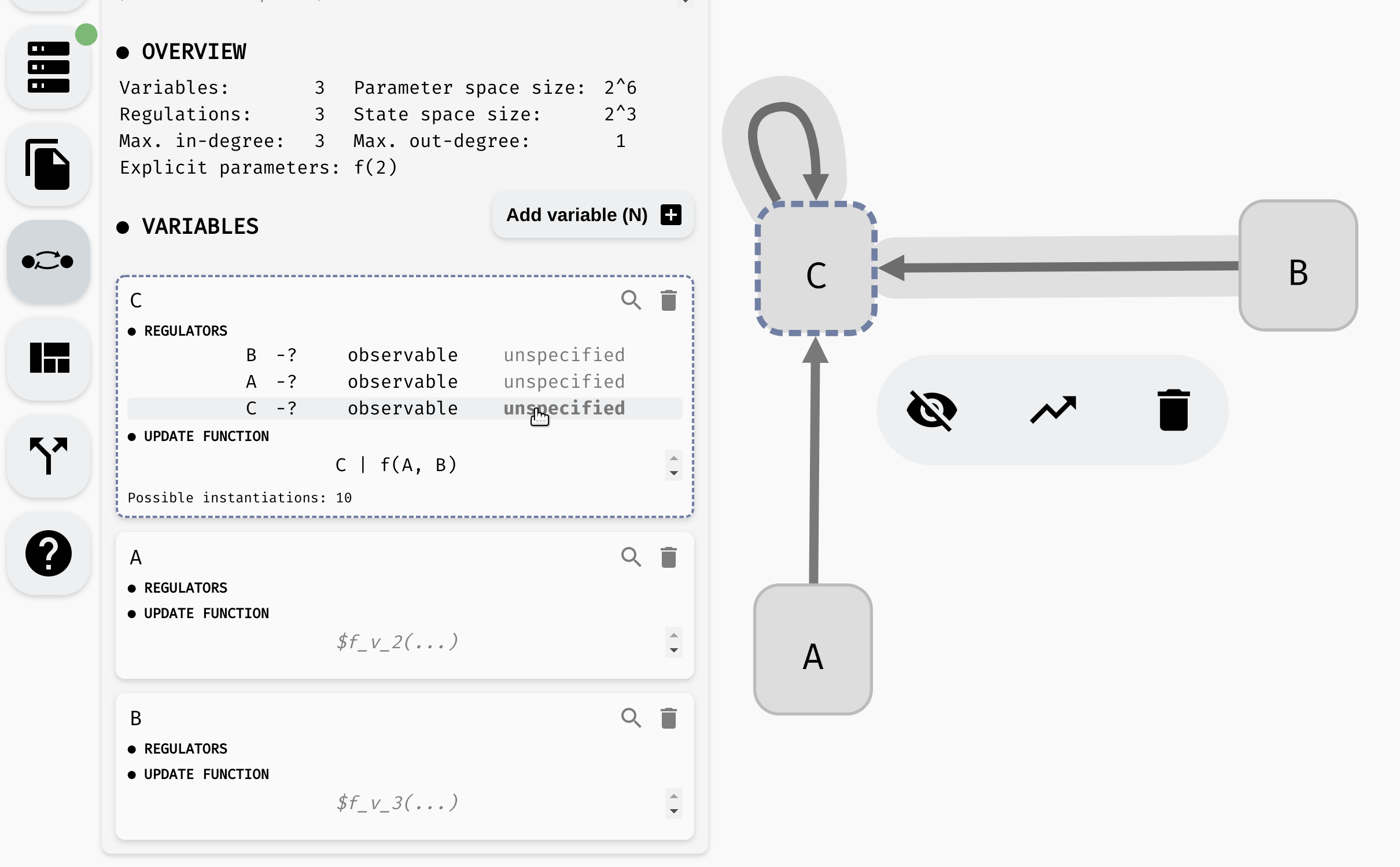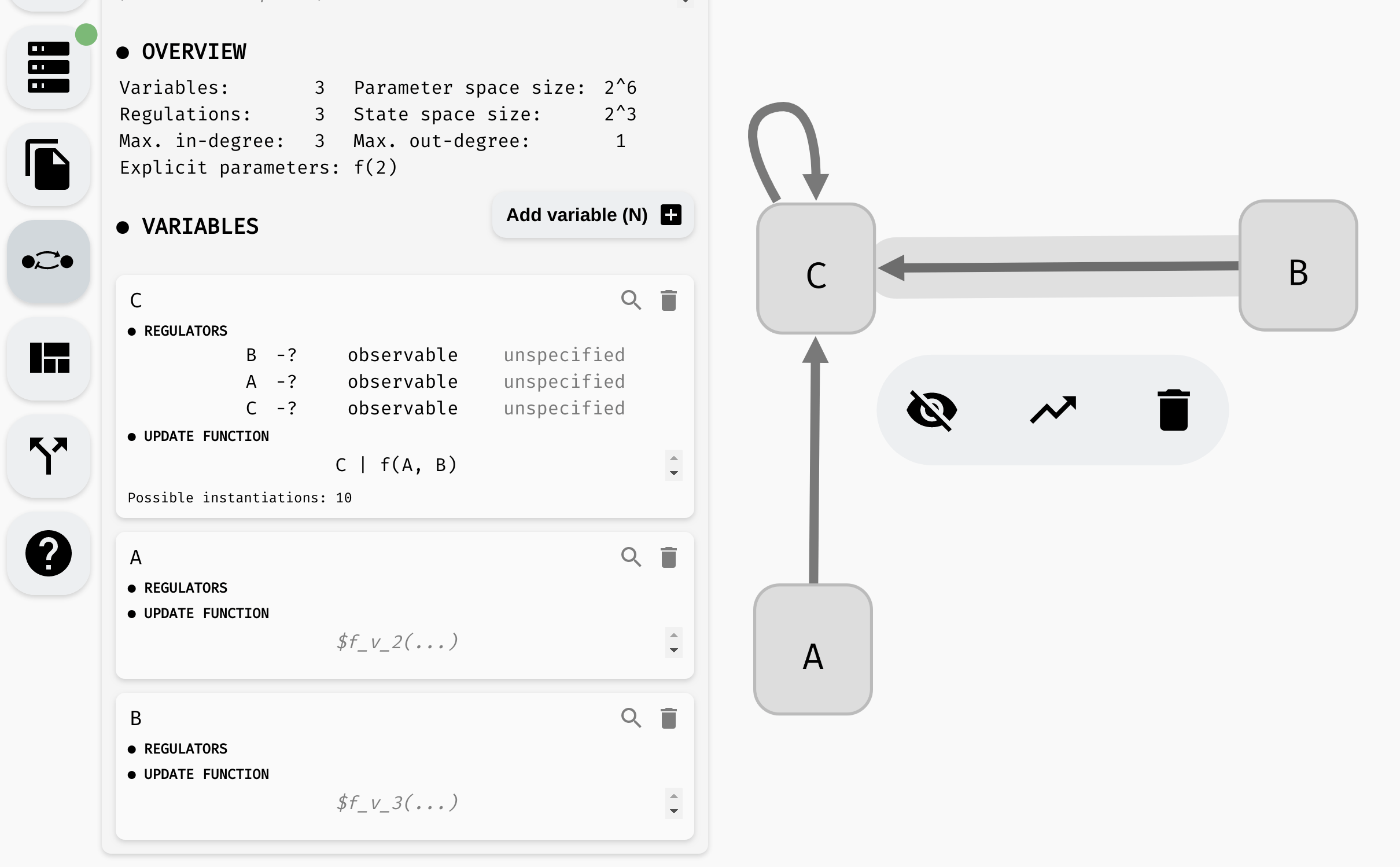Changing monotonicity of regulations.

Notice that as we change the monotonicity of a regulation, the number of instantiations of the update function also changes. This is because the number of Boolean functions with that specific property is smaller. Specifically, if a regulation is positively monotonous, we expect that increasing the value of the regulator cannot decrease the value of the output, and vice versa, when the monotonicity is negative, increasing the value of the regulator cannot increase the function output.

Specifically, if we set the regulation B -> C as activation, we reduce the number of instantiations of f(A, B) to only four options: A & B, !A & B, A | B, !A | B. In particular, notice that in each such function, B appears in its positive form (without negation). We could further limit the number of instantiations by also setting a monotonicity for the A -> C relationship.

The regulation C -> C is slightly different. The dependence C -> C is already fully specified in the update function. Changing the properties of the regulation therefore cannot change the number of instantiations. However, it can make the function completely invalid if the properties given by the regulatory graph do not match the properties of the update function. Since in our case, C appears positively in C | f(A, B), AEON reports an error when the regulation is marked as an inhibition, but is ok with either activation or unspecified monotonicity.

When possible, AEON will try to infer which regulation properties cause the function to be invalid. You can then update the properties accordingly.

AEON explains why a function is not consistent with its regulatory graph.

Observability

While it is often reasonable to expect each regulation to have some effect on the regulated variable, sometimes we may not be sure if a regulation is indeed (always) needed. In such case, we can mark the regulation as non-observable.

AEON will then also consider instantiations where the argument does not have any impact on the resulting function value. To set this property, you can again use either the regulation menu, or the model panel:

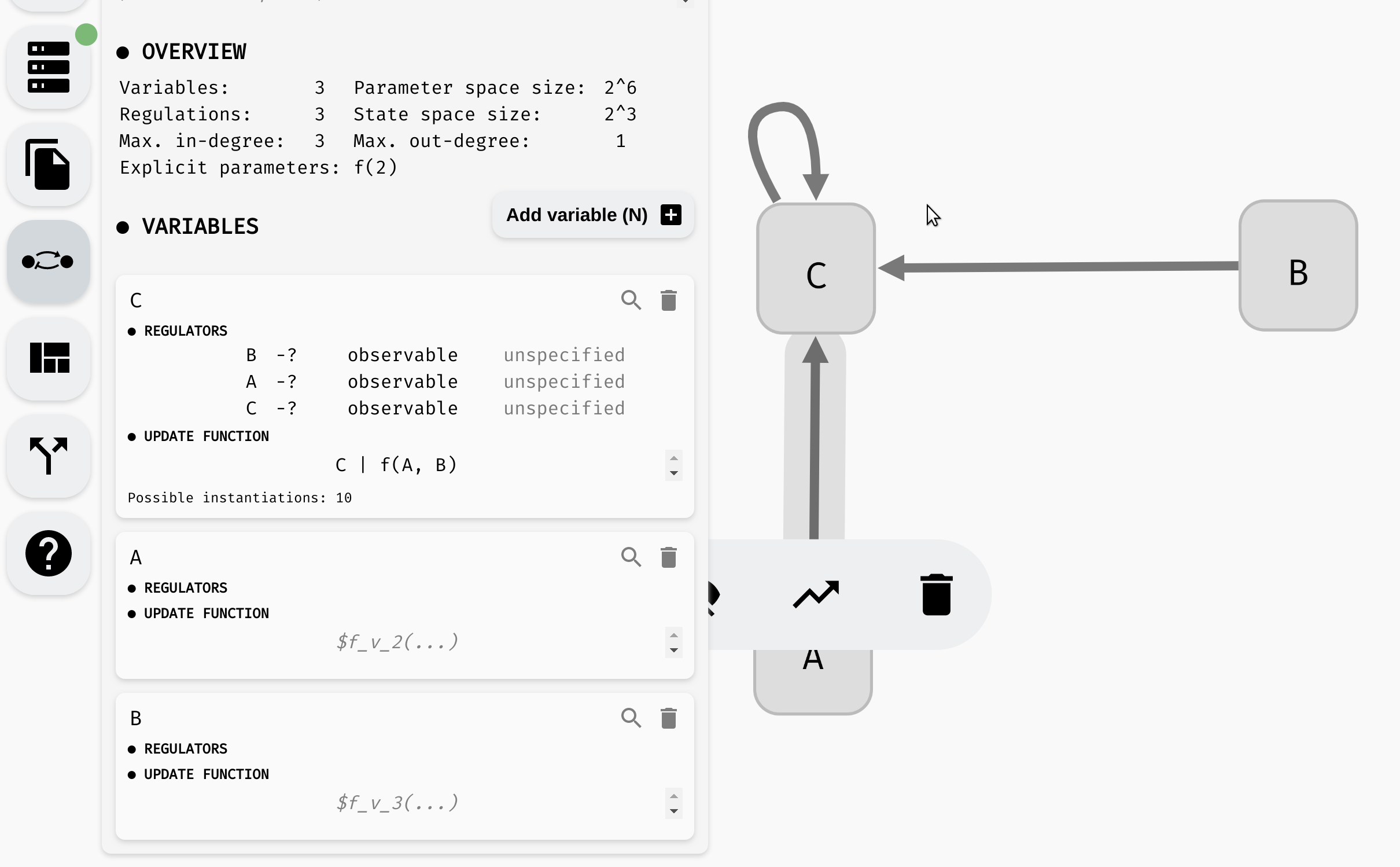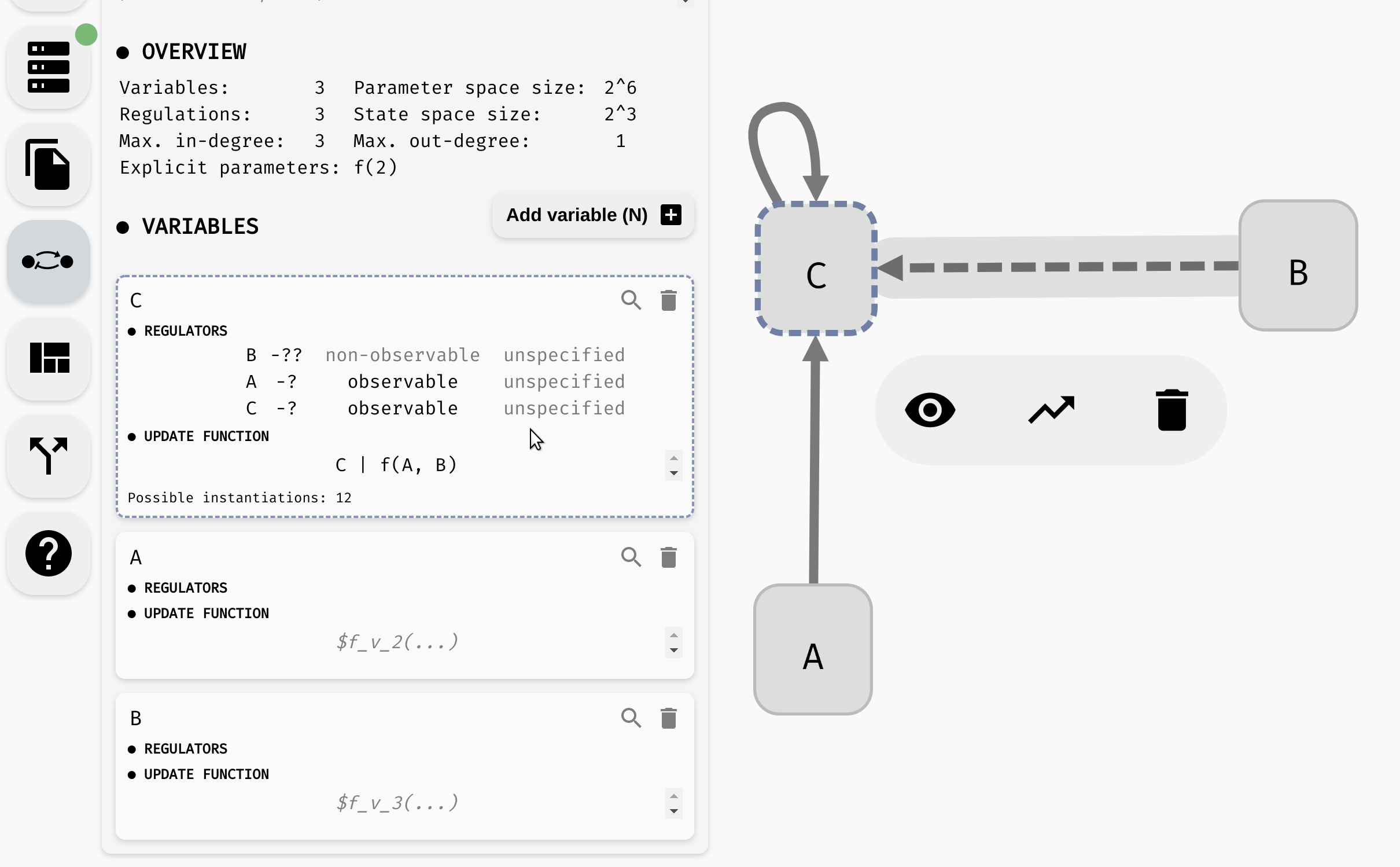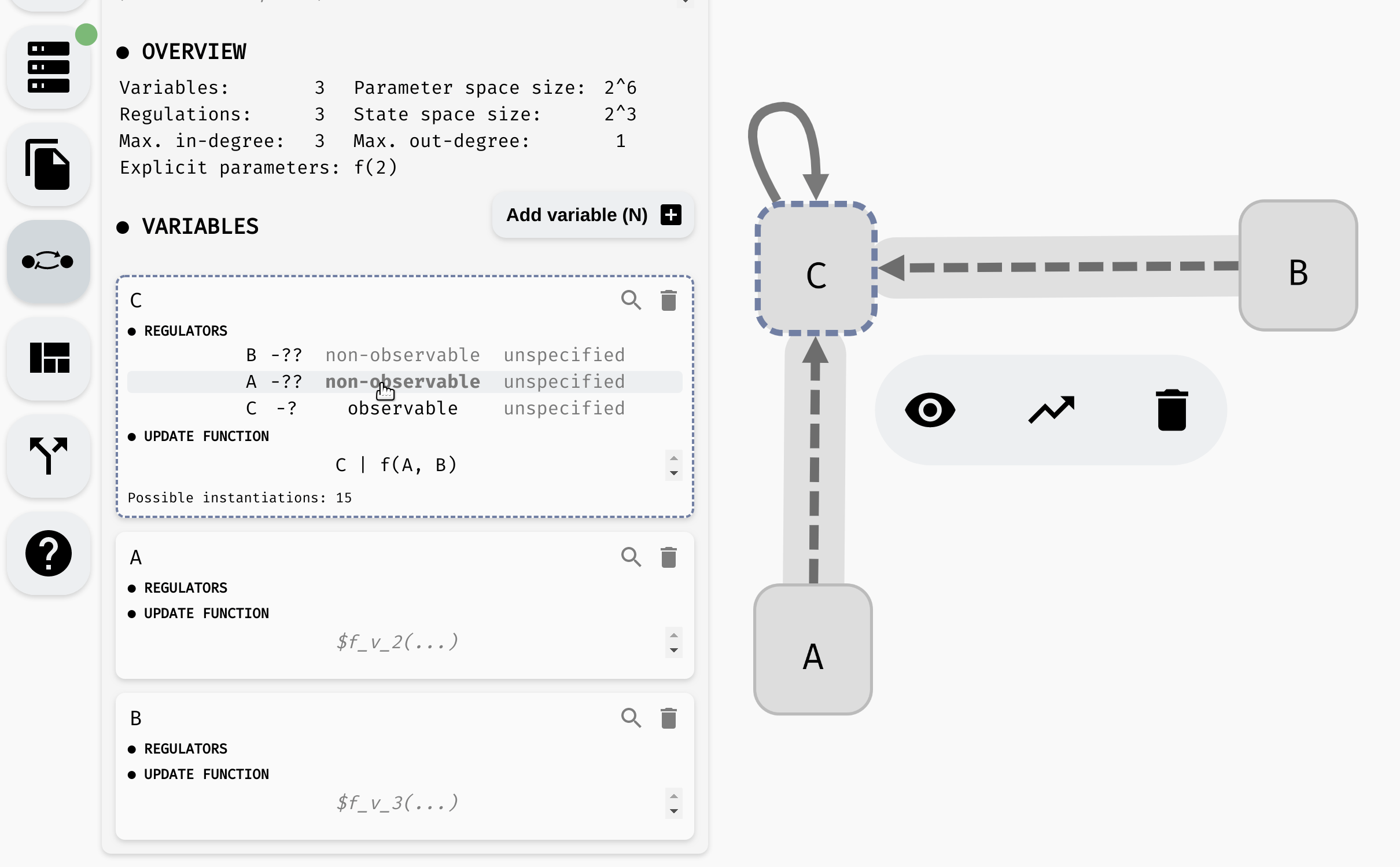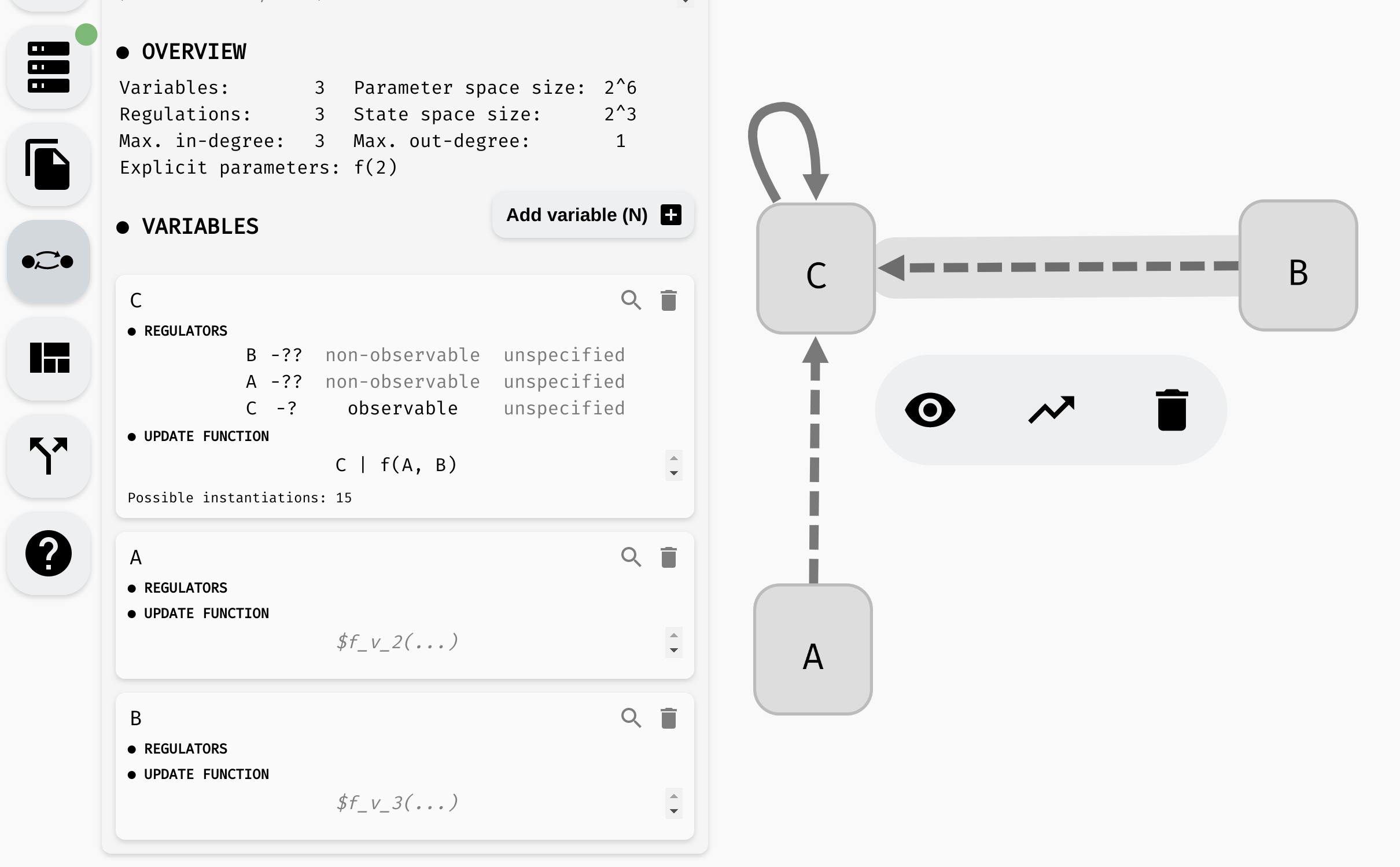Changing observability of regulations.

Notice that as we remove the observability requirements, the number of instantiations grows. In the end, the function has 15 possible instantiations. This includes all 16 possible binary Boolean functions except for one: true.

If we set f(A, B) = true, the update function would be C | true, which is equivalent to true. However, we still have C -> C marked as observable, and a constant function does not depend on C. Meanwhile, instantiation f(A, B) = false is fine, because C | false is equivalent to C, which clearly still depends on the value of C.

Also, note that a function can "appear" to depend on a value of some variable, while in fact it does not. Take a simple example of (A & B) | A. If A=true, this function is always true, if A=false, this function is always false, regardless of the value of B. AEON will also detect and report these types of problems.

Inconsistencies in real world models

Note that in many cases, you can encounter real-world models where AEON identifies some structural inconsistencies as described in this section. In such case, you cannot directly analyse the original model.

This does not necessarily mean the model is incorrect, but it can suggest some kind of human error (a missing negation, wrong parenthesis, etc.), or an inconsistency between experimental data and literature (regulatory graph is often constructed based on known assumptions about the system, prior to the actual Boolean functions).

In such case, assuming you cannot consult the author(s) of the model about the inconsistency, we recommend simply updating the regulatory graph to make it consistent with the update functions in the model. That is, removing the monotonicity or observability requirement from the problematic regulation.

Import/Export

Finally, lets discuss how to transfer your models into AEON, as well as sharing them with the world afterwards. AEON has an Import/Export panel accessible in the left menu:

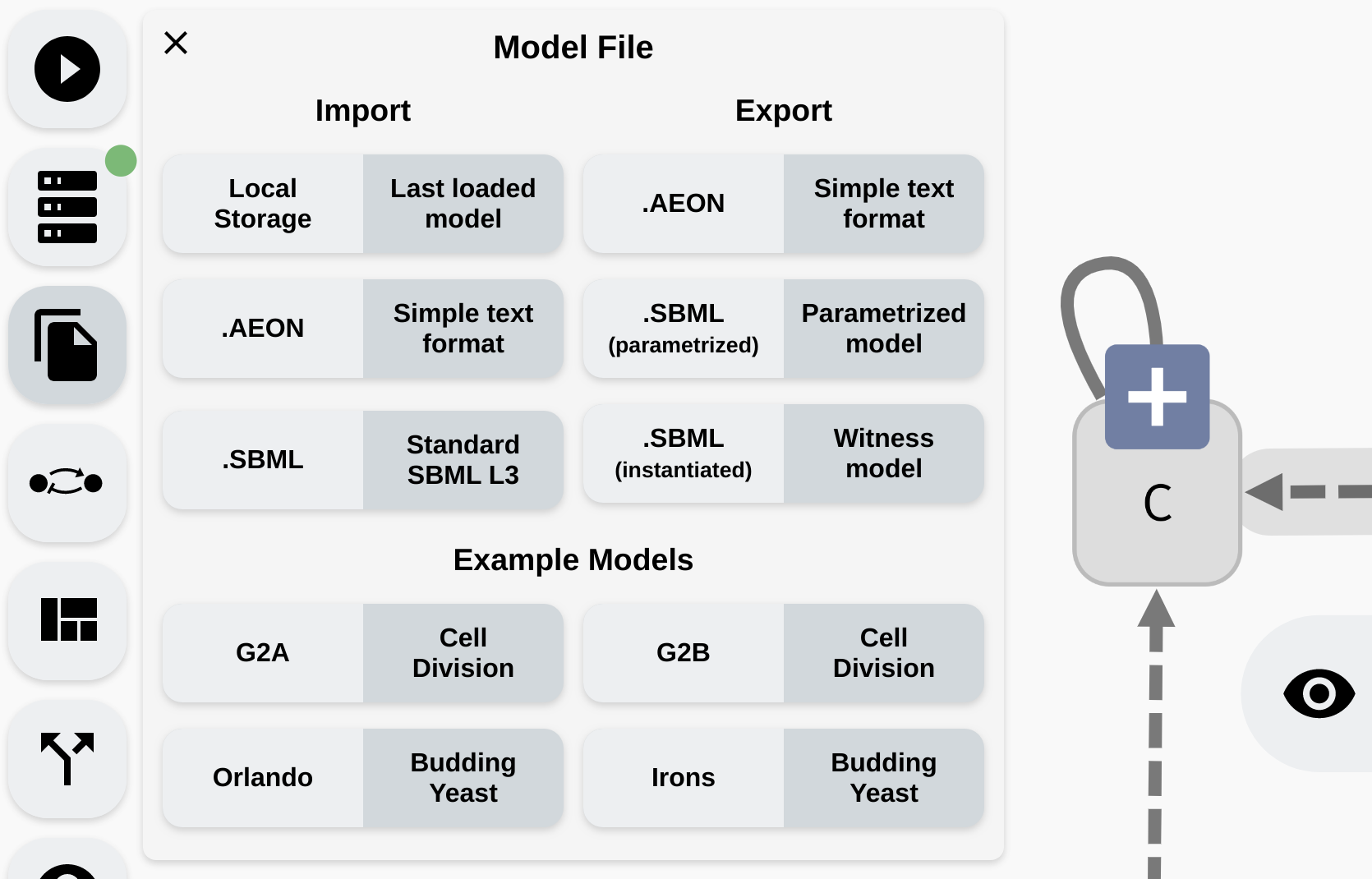Import/Export panel in AEON.

At the bottom, you can see a collection of four pre-defined example models which you can open to demo AEONs functionality. Each model contains additional description of its properties.

The Local Storage option tries to continuously save the model you are working on into the local storage of your browser. If you accidentally reload your editor and lose some unfinished work, you can try to recover it from this local storage.

SBML-qual

AEON should be fully compatible with SBML-qual models. You can therefore both import and export .sbml models from AEON. However, there are a few restrictions to keep in mind:

• AEON only supports alphanumeric names with underscores, while SBML also supports other special characters (for example[]). During import, AEON will replace all conflicting characters with underscores. If this leads to a name clash, it also adds a unique ID to the name of each variable.
• AEON will try to import layout information from the SBML file, but the layout may be incompatible (some tools use a [0,1] coordinate system, which makes the layout very small), or completely missing. In such case, all variable nodes will appear at the same position. You can then apply the automatic layout to better visualise the network.
• SBML does not have explicit support for observability. If a regulator appears in an update function, AEON will import this regulation as observable. If the regulator is completely missing in the function, it will be imported as non-observable.
• SBML may contain variables with unspecified update functions. These are naturally imported as implicitly parametrised. However, there is no support for explicit parameters. To implement this functionality, if a model contains explicit parameters, we export the update function with a <csymbol> MathML element (used to denote arbitrary function invocation). This can be imported back into AEON, but won't be interpretable in other tools that follow the SBML standard. You can disable this behaviour by using the SBML (instantiated) button. In this mode, AEON will pick some arbitrary instantiation for each parameter and thus export a valid SBML.

Aeon format

Since SBML is quite hard to edit by hand, as well as parse correctly, we also provide a simplified text based format. In this format, the regulatory graph is described as a list of edges, where each edge is encoded as regulator [->,-|,-?,->?,-|?,-??] target. Here, regulator and target are the names of the network variables, and the arrow connecting them describes the type of regulation. Then -> denotes activation, -| inhibition and -? is unspecified monotonicity. Finally, an extra ? signifies that the regulation is non-observable.

An update function for variable X is written as $A: function, where the format of the actual functions in .aeon files is the same as in the edit fields in the AEON interface. Additional information (model name, description and layout) is encoded in comments (lines starting with #). The order of declarations is not taken into account. Example of .aeon model:

    #name:Asymmetric Cell Division A
    #description:Lorem Ipsum....
    #position:CtrA:419,94
    CtrA -> CtrA
    GcrA -> CtrA
    CcrM -| CtrA
    SciP -| CtrA
    $CtrA: CtrA & GcrA & !CcrM & !SciP
    #position:GcrA:325,135
    CtrA -| GcrA
    DnaA -> GcrA
    $GcrA: !CtrA | DnaA
    #position:CcrM:462,222
    CtrA -> CcrM
    CcrM -| CcrM
    SciP -| CcrM
    $CcrM: CtrA | f(CcrM, SciP)
    #position:SciP:506,133
    CtrA -> SciP
    DnaA -| SciP
    #position:DnaA:374,224
    CtrA -> DnaA
    GcrA -| DnaA
    DnaA -| DnaA
    CcrM -> DnaA
    $DnaA: g(CtrA, GcrA, DnaA) & CcrM

Note that due to this encoding, .aeon technically can't represent a variable with no incoming or outgoing regulations. Such variable may be lost during export.

Attractor Bifurcation

In this chapter, you will learn how to study the long term behaviour of Boolean networks using AEON. Specifically, we refer to this analysis as attractor bifurcation, because it examines how parameters influence the long term behaviour (attractors) of a particular Boolean network.

Attractors are subgraphs of the asynchronous state transition graph of the Boolean network. Recall that this graph consists of states which assign Boolean value to each variable of the network, and transitions which correspond to applications of individual update functions. Then, attractor consists of states that, once reached, cannot be escaped. Informally, these are the regions where the network eventually converges to, and stays forever. In terms of graph theory, these are the bottom (terminal) strongly connected components of the state transition graph.

In AEON, we distinguish between three main types of attractors:

• Stable attractor is an attractor which consists of a single state. This type of attractor is also called a sink.
• Oscillating attractor is a cycle of states. The length of the cycle is its period, hence this type of attractor is sometimes also referred to as periodic.
• Disordered attractor is an arbitrary set of states consisting of multiple connected cycles. This type of attractor is also called aperiodic.

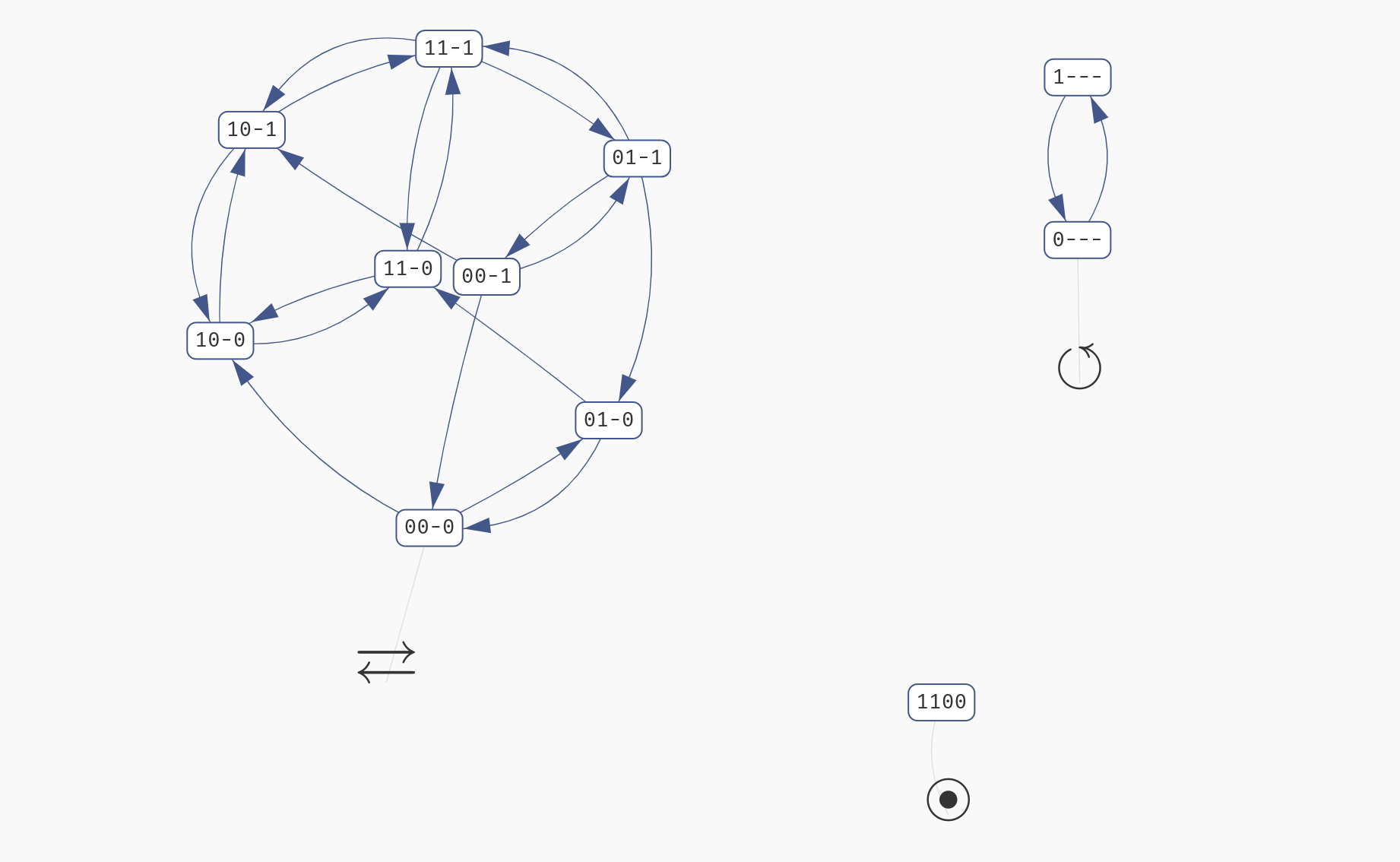Three types of attractors. Notice that each type is labelled with an appropriate icon.

To compute the attractors of the network, click Start Analysis in the left menu. Keep in mind that for large models (especially with a lot of parameters), this process can take a long time. The compute engine color should change to orange, and you should find a (very) approximate progress of the computation in the compute engine panel. Here, you can also cancel the current computation.

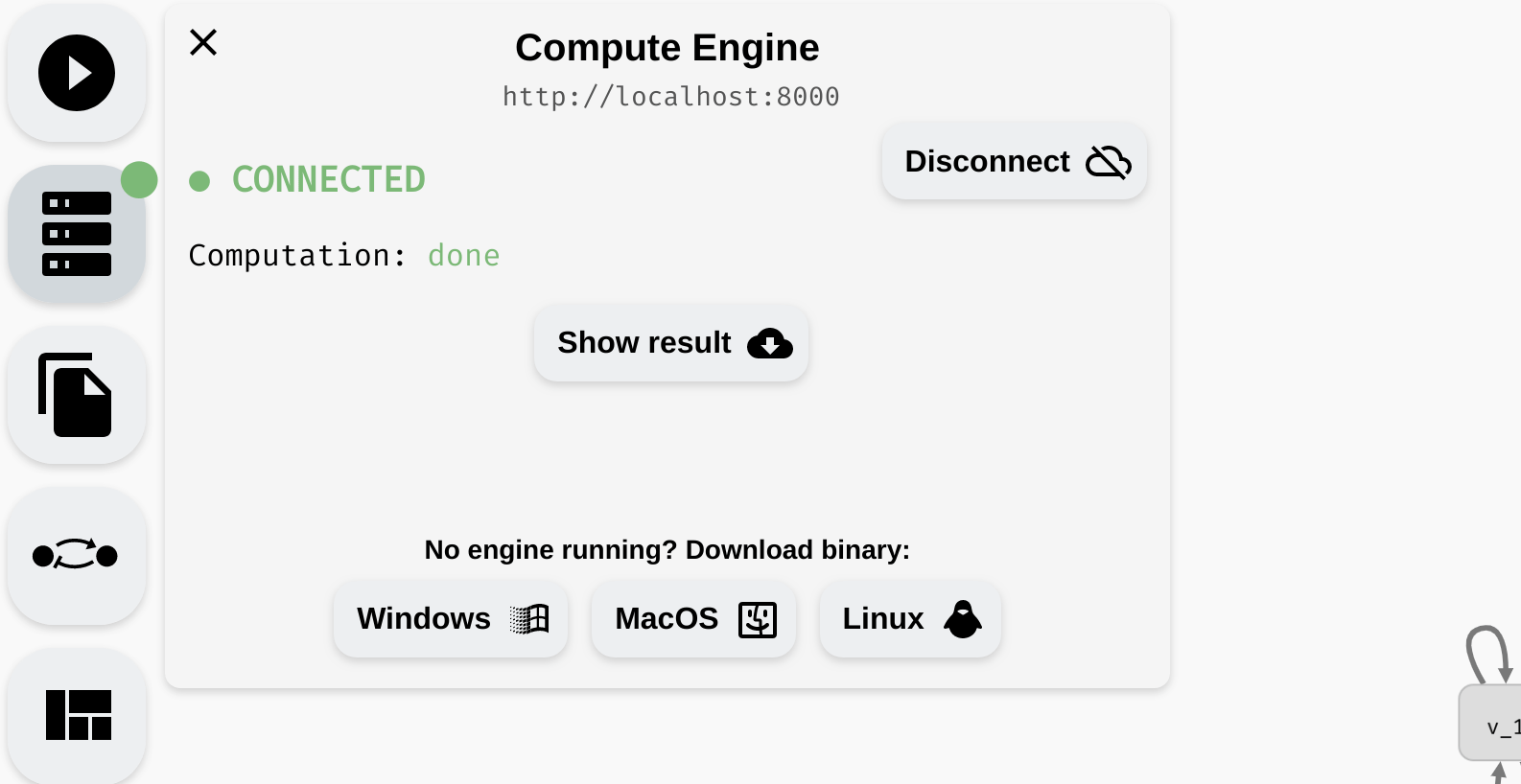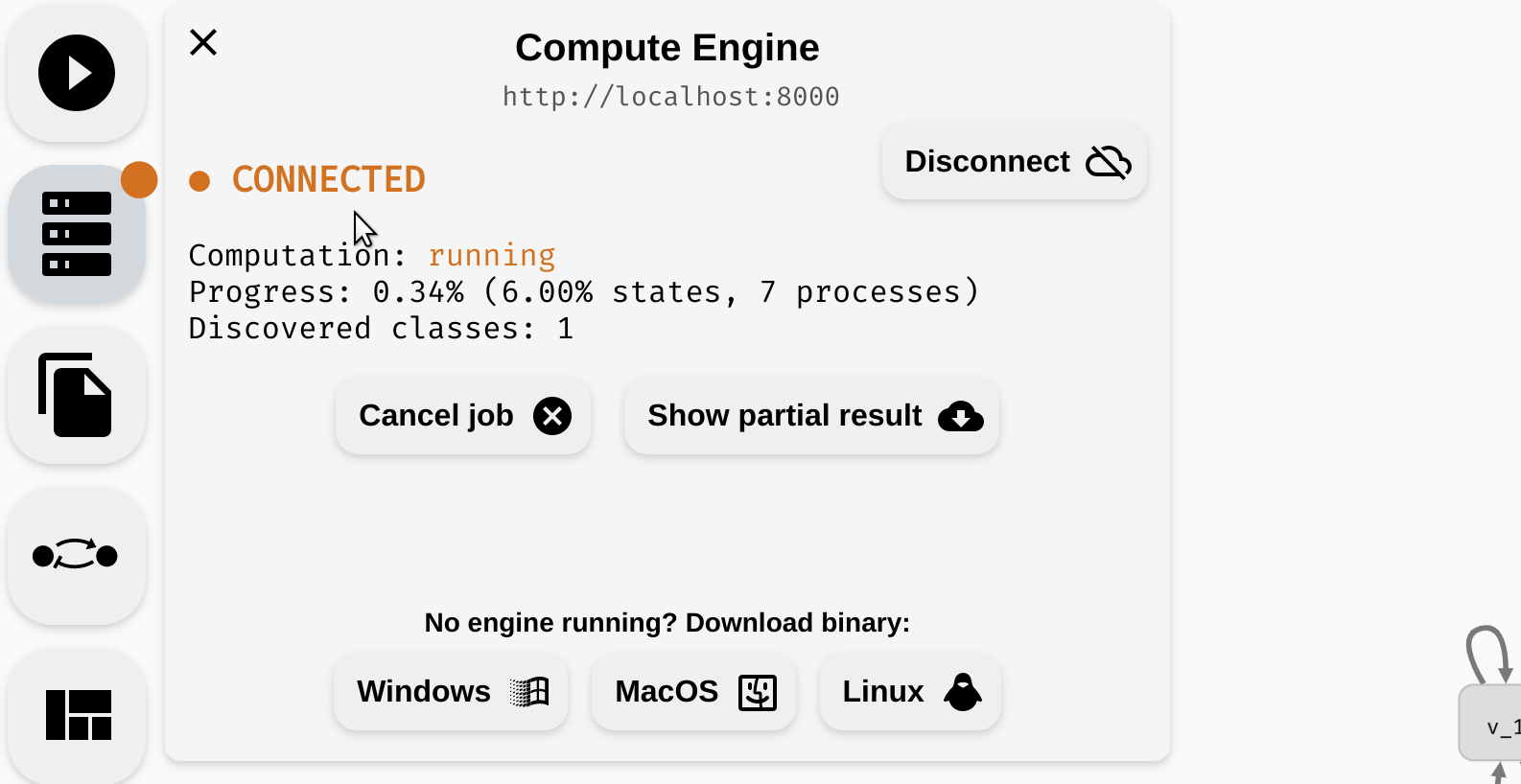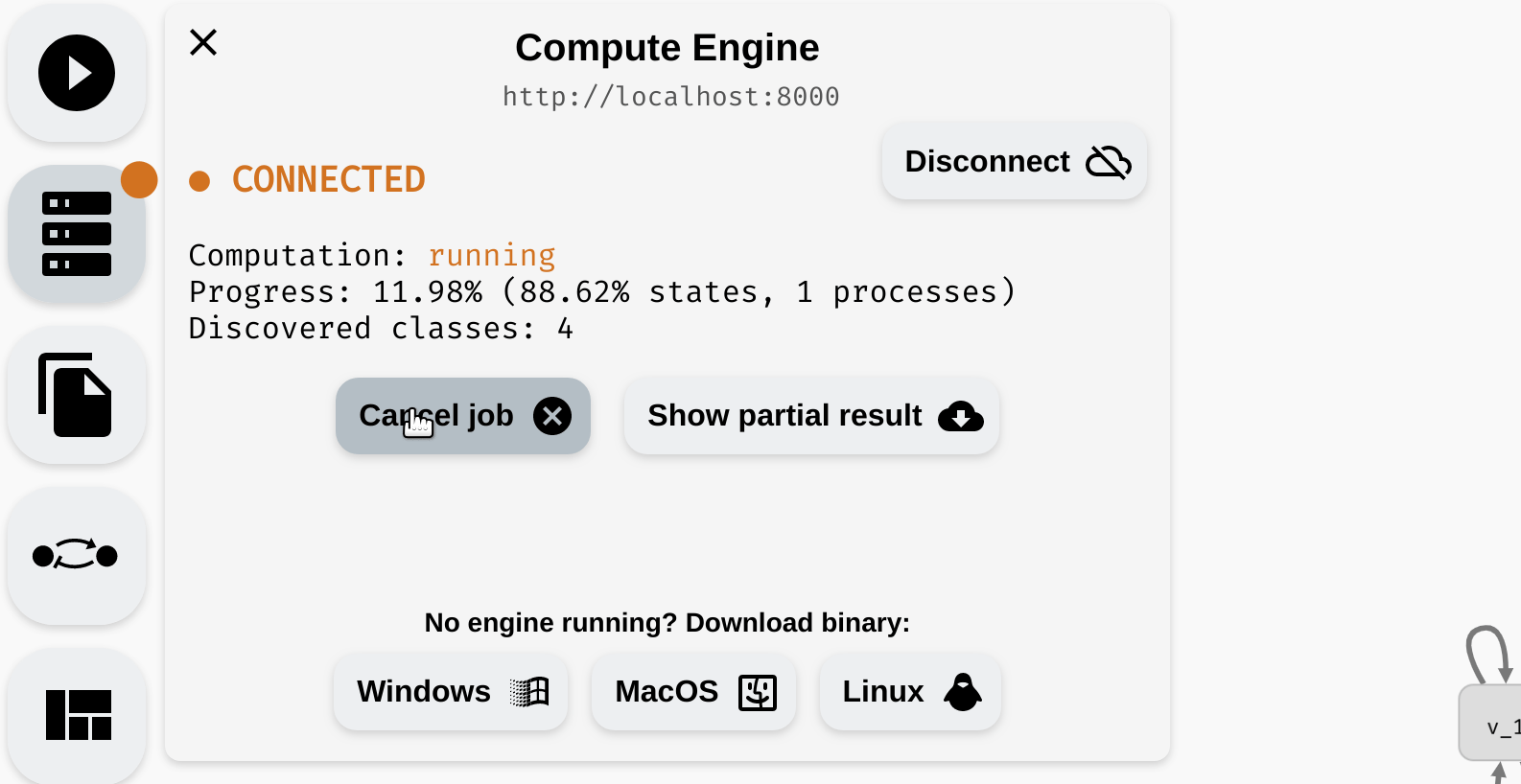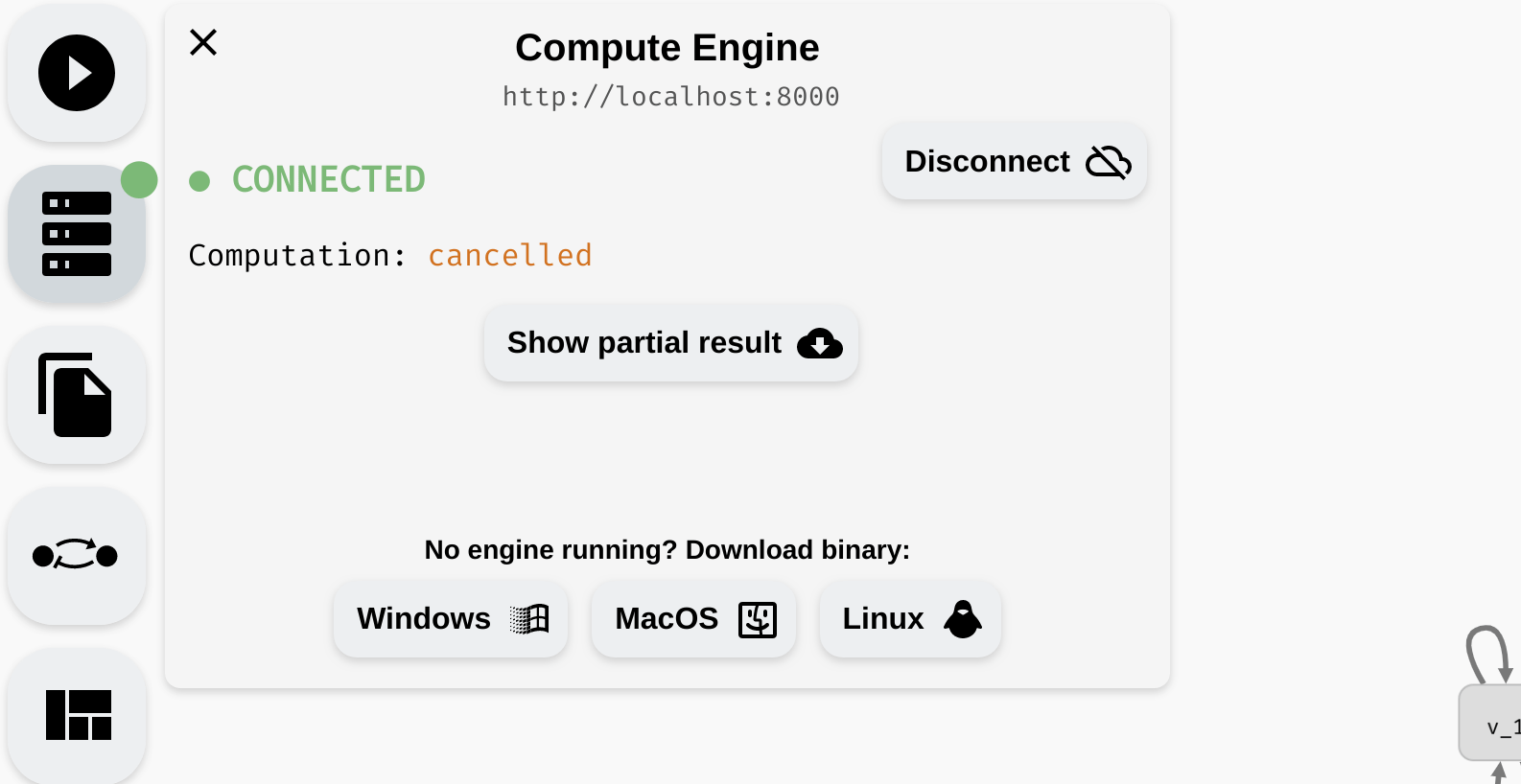Starting and cancelling a computation.

Due to the nature of the problem, it is typically not possible to accurately predict how long it will take to compute the results. The progress corresponds to the number of states eliminated as "non-attractor" states so far, however, this is only meaningful when the attractors are relatively small. Also, as discussed previously, AEON compute engine can only run one computation at a time. If you need to run multiple experiments simultaneously, we recommend running multiple compute engines.

Once the computation is finished, you should be taken to the Results panel, where you can see the overview of the attractor bifurcation function. If your model has no parameters, the function has one row showing the types of attractors in your network (behaviour class). In a parametrised model, there are usually multiple rows, each showing you the number of parametrisations (witness count) which produce a specific type of behaviour.

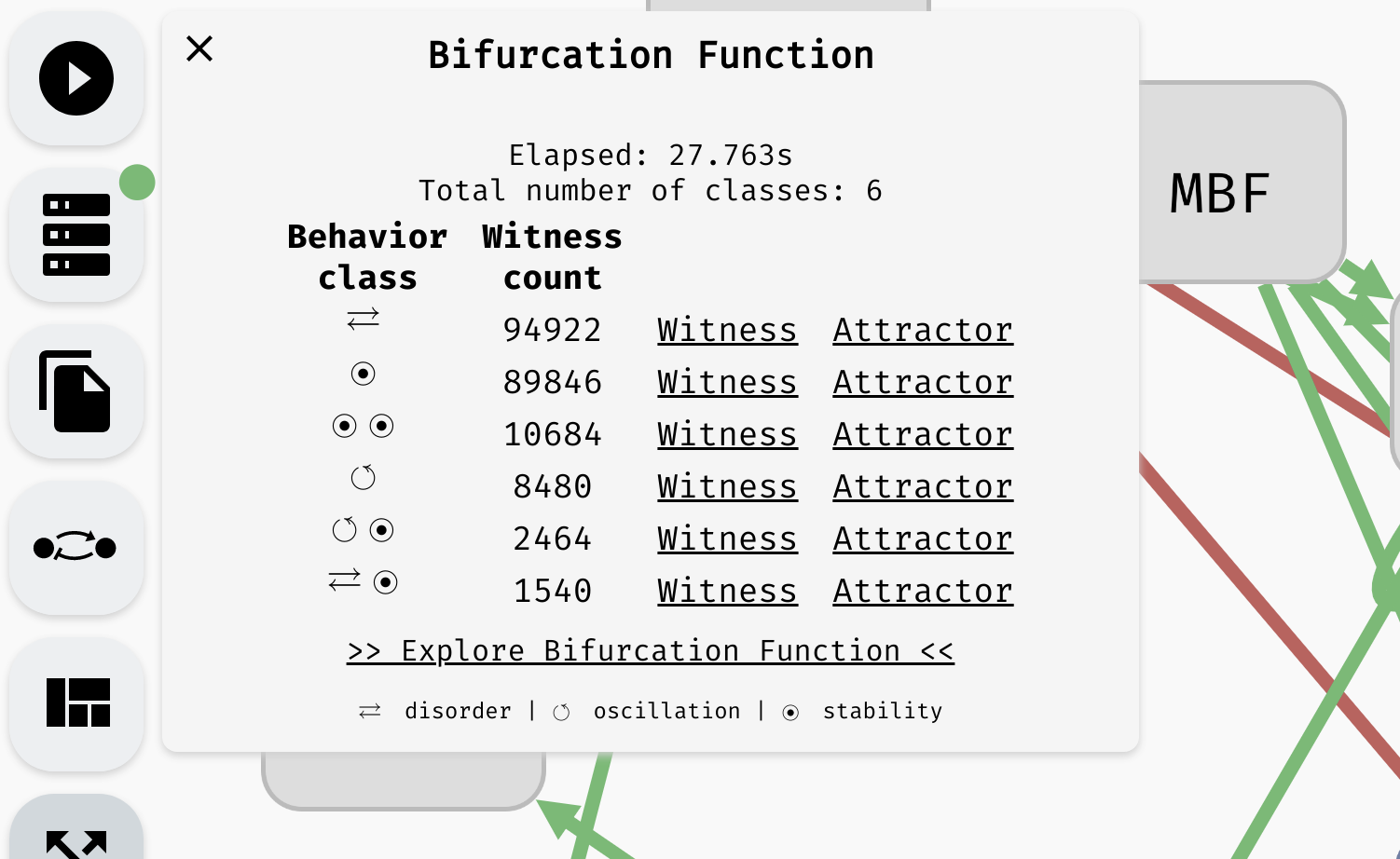An overview of an attractor bifurcation function of a parametrised Boolean network. There are 6 behaviour classes, two having an oscillating attractor and two having a disordered attractor. Remaining attractors are stable.

Note that the attractors that fall into the individual behaviour classes may not have identical state space. Only their type is equivalent. For example, a class with a single stable attractor can actually cover many distinct stable states. However, in every parametrisation (for that class), AEON guarantees there is exactly one stable state. You can then use stability analysis to examine how the values of variables differ in various conditions.

From here, you can continue in different directions:

• You can generate a Witness for each behaviour class. This is a fully specified Boolean network (no parameters) that exhibits the attractors as described by the behaviour class.
• You can explore the state space of the discovered attractors by clicking Attractors.
• You can explore the dependence between attractors and behaviour classes using a decision tree (Explore Bifurcation Function).
• You can examine stable/unstable/switched variables in the attractors of a particular behaviour class (Explore Bifurcation Function).

We discuss these methods in the following sections.

State space explorer

If you click the Attractors button in the Results panel, a state space explorer appears with the exact representation of the attractors discovered in the network for that particular behaviour class.

You can click each state to see a breakdown of the variables which are true (green) or false (red) in said state. In an oscillating or disordered attractor, the state labels will contain a dash (-) in place of variables which have a fixed (stable) value in the whole attractor. They will be also shown as grey in the variable values list. This way, you can quickly visually distinguish which variables are fixed and which are being updated in the attractor.

However, if your network is parametrised, remember that this visualisation always shows attractors of a fully specified Boolean network that was picked from the particular behaviour class. That is, state space of attractors in other parametrisations can be different. To show the update functions used in this particular network, you can click the Function button in the top left.

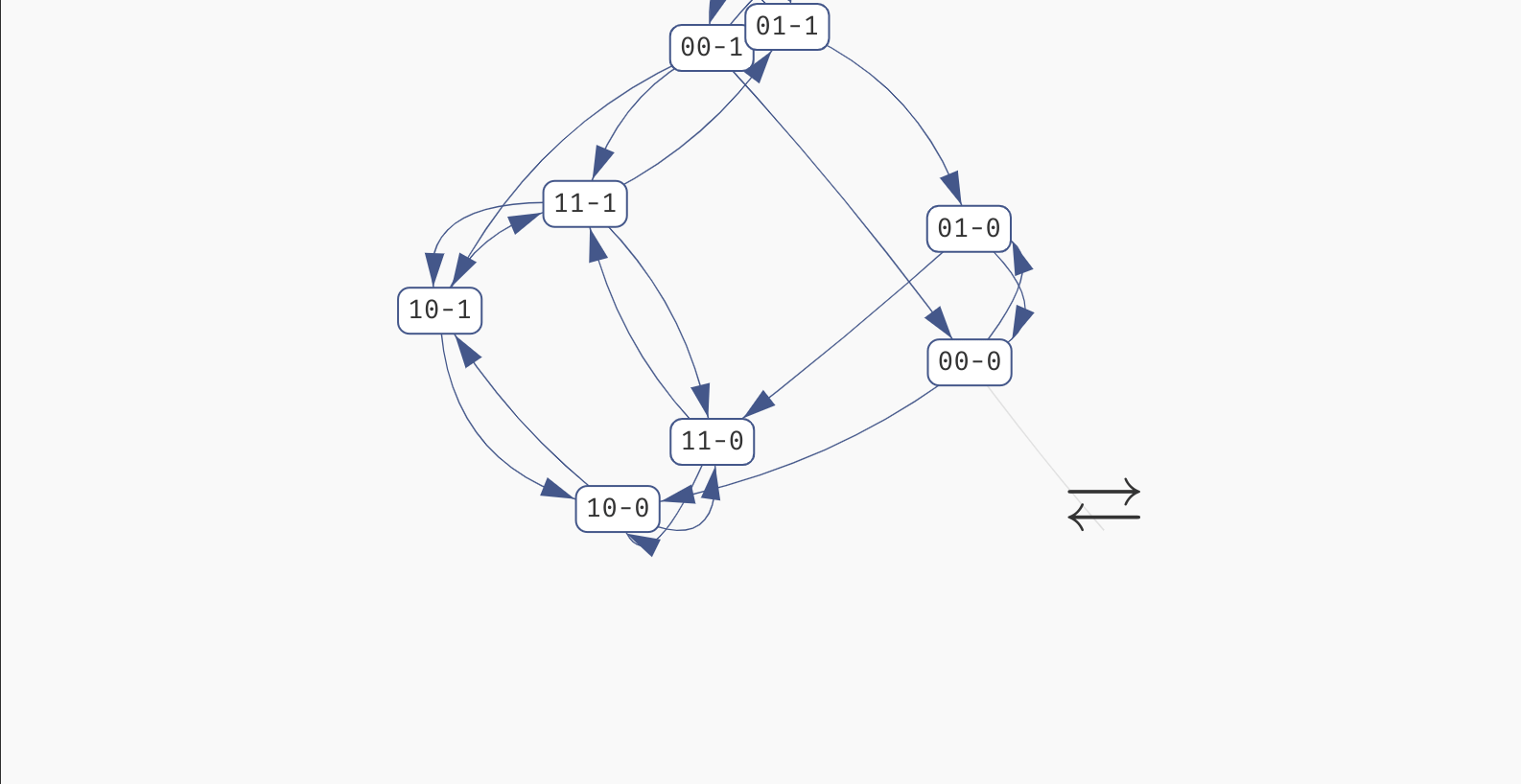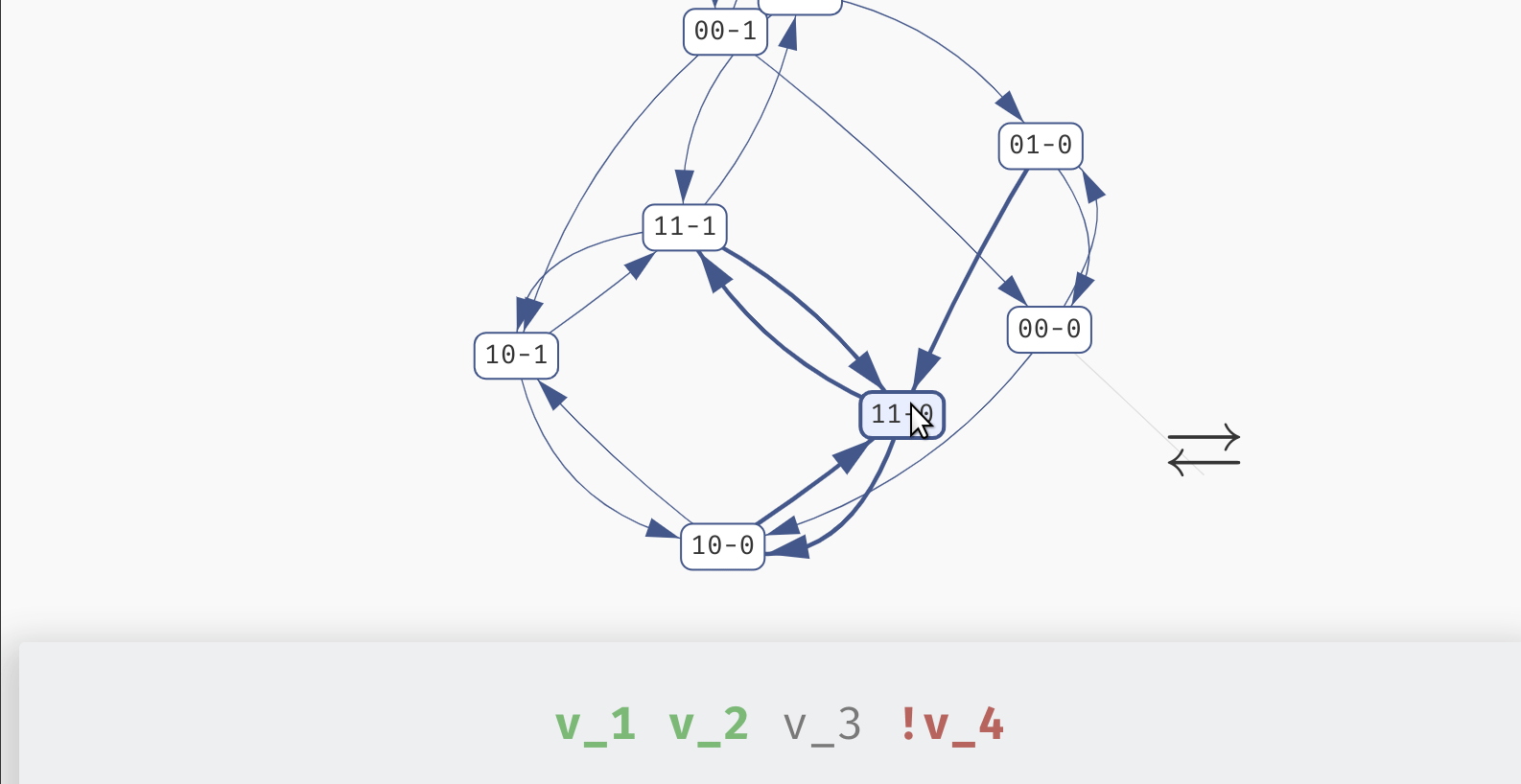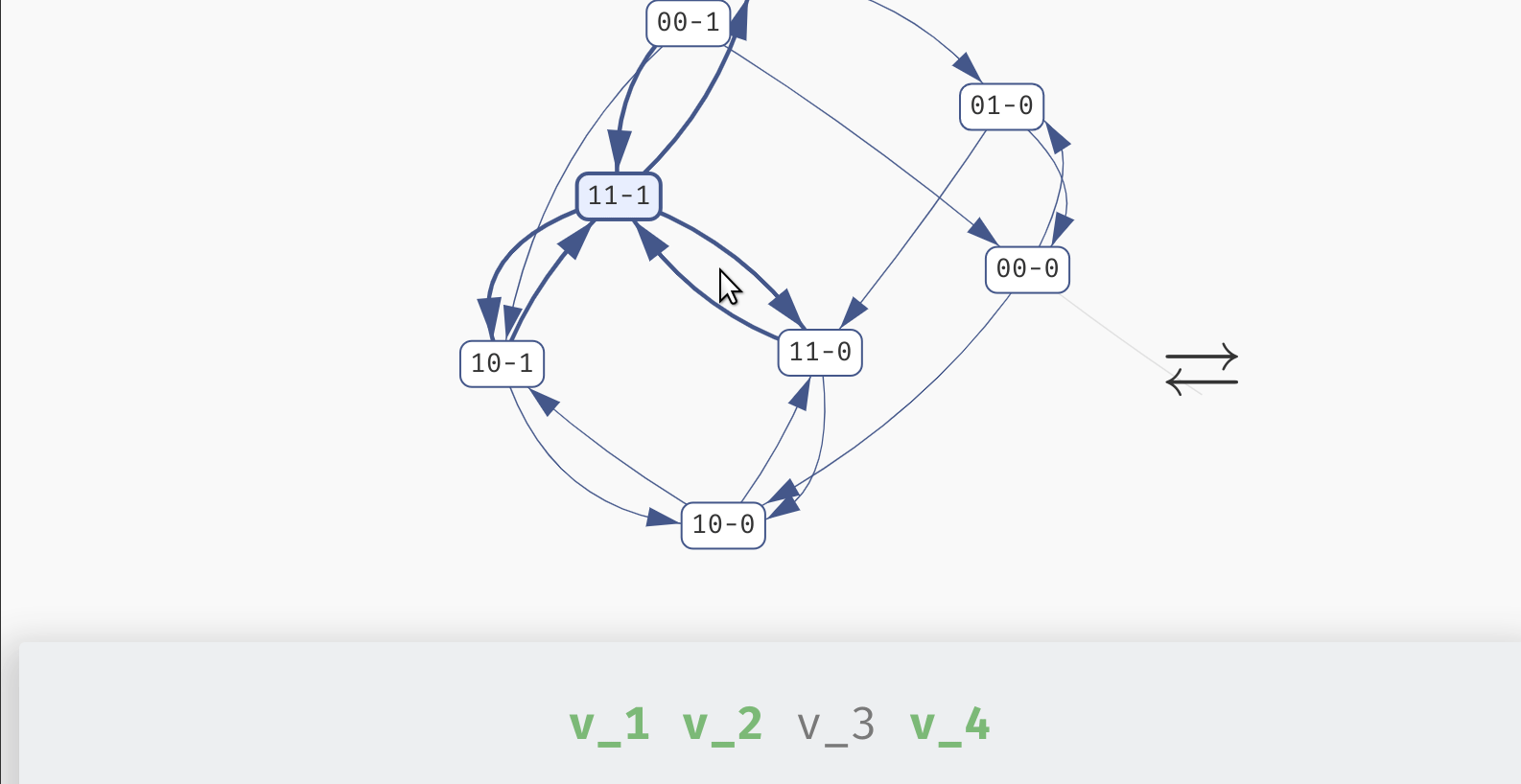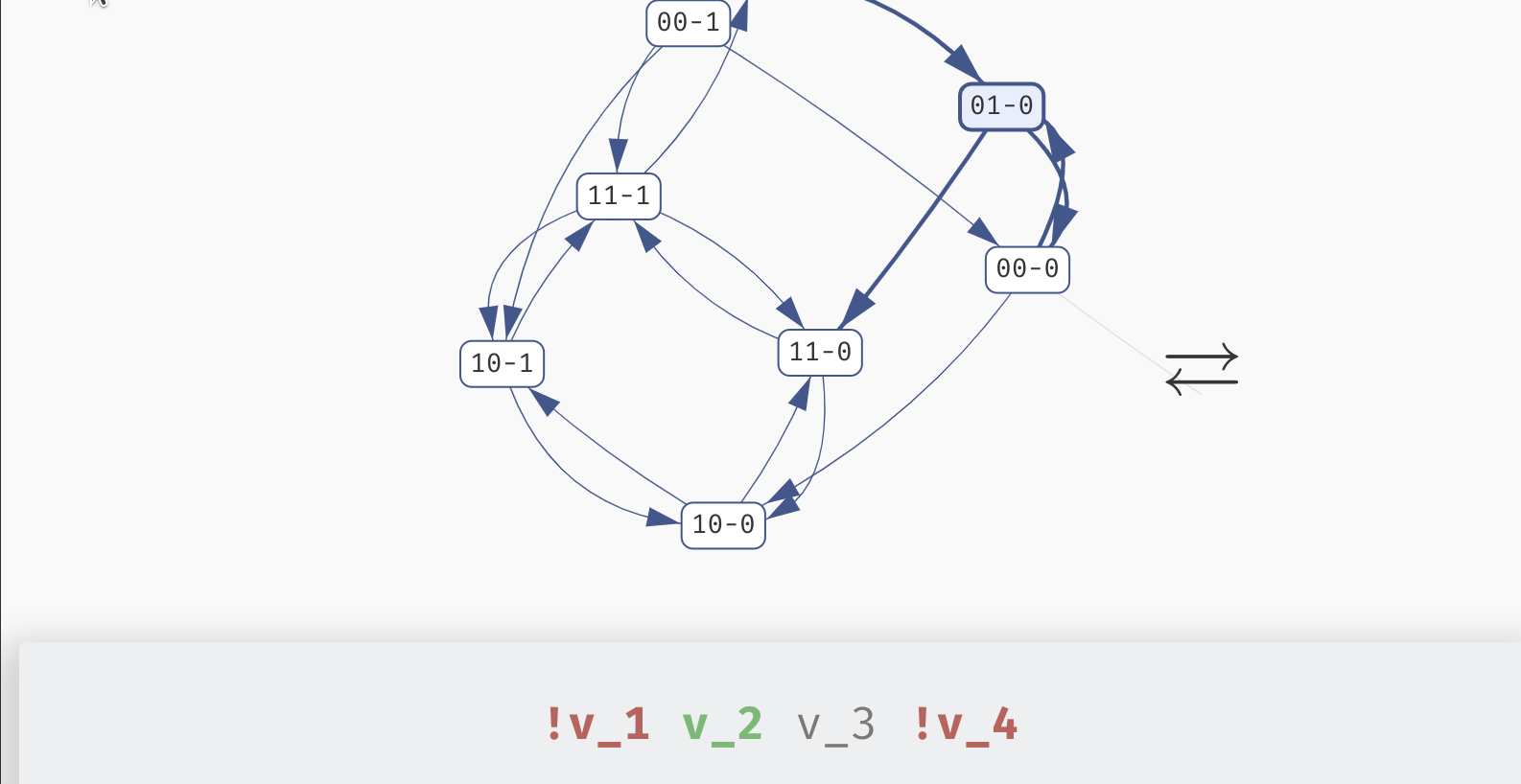Exploring the states of a disordered attractor.

Keep in mind that in a large network, you can use the Find... functionality of your browser to quickly highlight the important variables in the list of variable values.

Finally, if the attractor is very large (approx. >5.000 states), we can't easily display it in a browser. We thus only show a simplified view of the attractor compressed into two states. In these two states, the stable variables have the values with which they appear in the attractor, and the unstable values simply all switch between true and false in one transition:

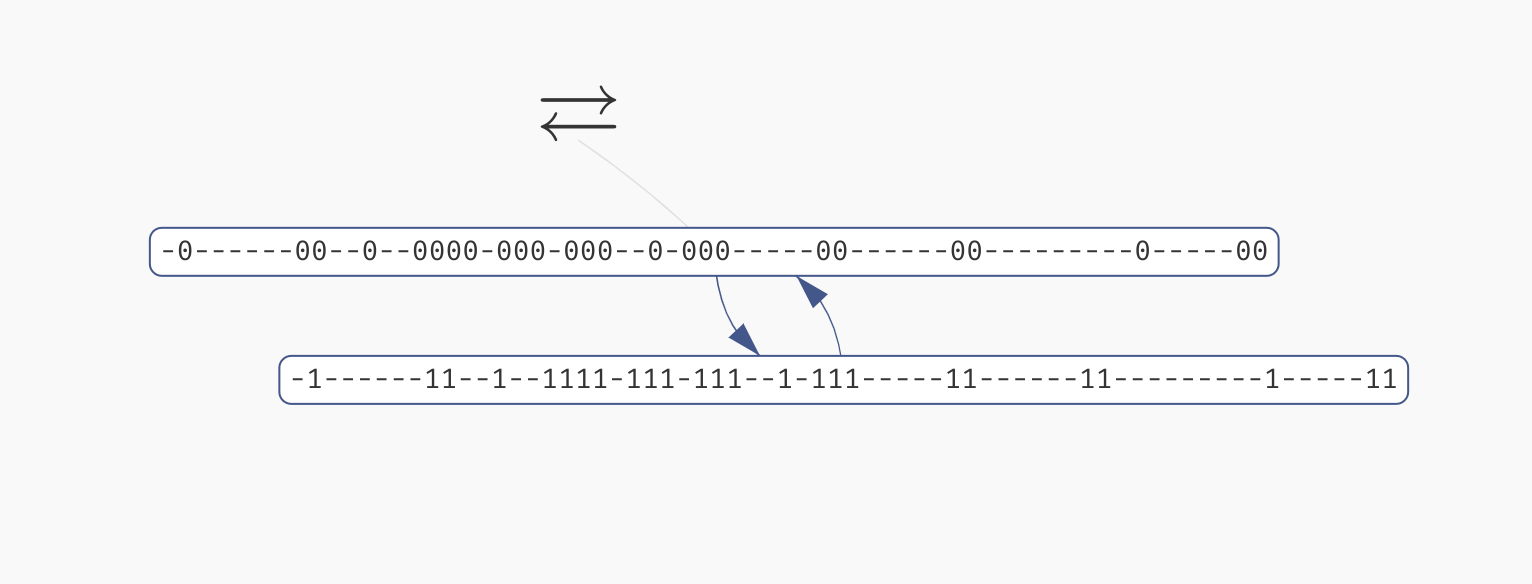A view of a large compressed attractor.

Bifurcation decision trees

To follow along with this section, you can download the .aeon model we will be using here. After loading it into AEON, you should see that the model has 66 variables and 13 parameters. Here, the parameters correspond to the input nodes of the regulatory graph, i.e. variables with no incoming regulations. Computing attractors for this model should take somewhere between 30 and 60 seconds.

The model can exhibit two behaviour classes: One with a stable attractor, and one with a disordered attractor. However, it is not clear which conditions lead to these two different classes! To explore this further, open the Bifurcation Function Explorer.

In this window, we will be constructing a bifurcation decision tree which describes how parameters alter the behaviour of the network. This decision tree consists of three types of nodes:

• A leaf node corresponds to a set of parametrisations which admit only a single behaviour class.
• A mixed node corresponds to a set of parametrisations which admit multiple behaviour classes.
• A decision node splits the parametrisations based on a value of a specific parameter.

Our goal will be to gradually turn mixed nodes into leaf or decision nodes to uncover which parameters influence the presence of different attractors in the network.

Initially, the tree contains a single mixed node with all admissible parametrisations of the network. By clicking the node, we reveal an overview similar to the Results panel in the main AEON window. However, we can also turn this mixed node into a decision node using the Make Decision button. This button will cause AEON to compute possible impact of picking different parameters as decision attributes. You will then be presented with a list of attributes (i.e. parameters) that you can use to split the mixed node into two. For each decision attribute, AEON shows you the impact of that decision on the behavior classes in the mixed node. If the decision isolates one behaviour class from the rest, a leaf node with that class will appear. Otherwise, a new mixed node is created.

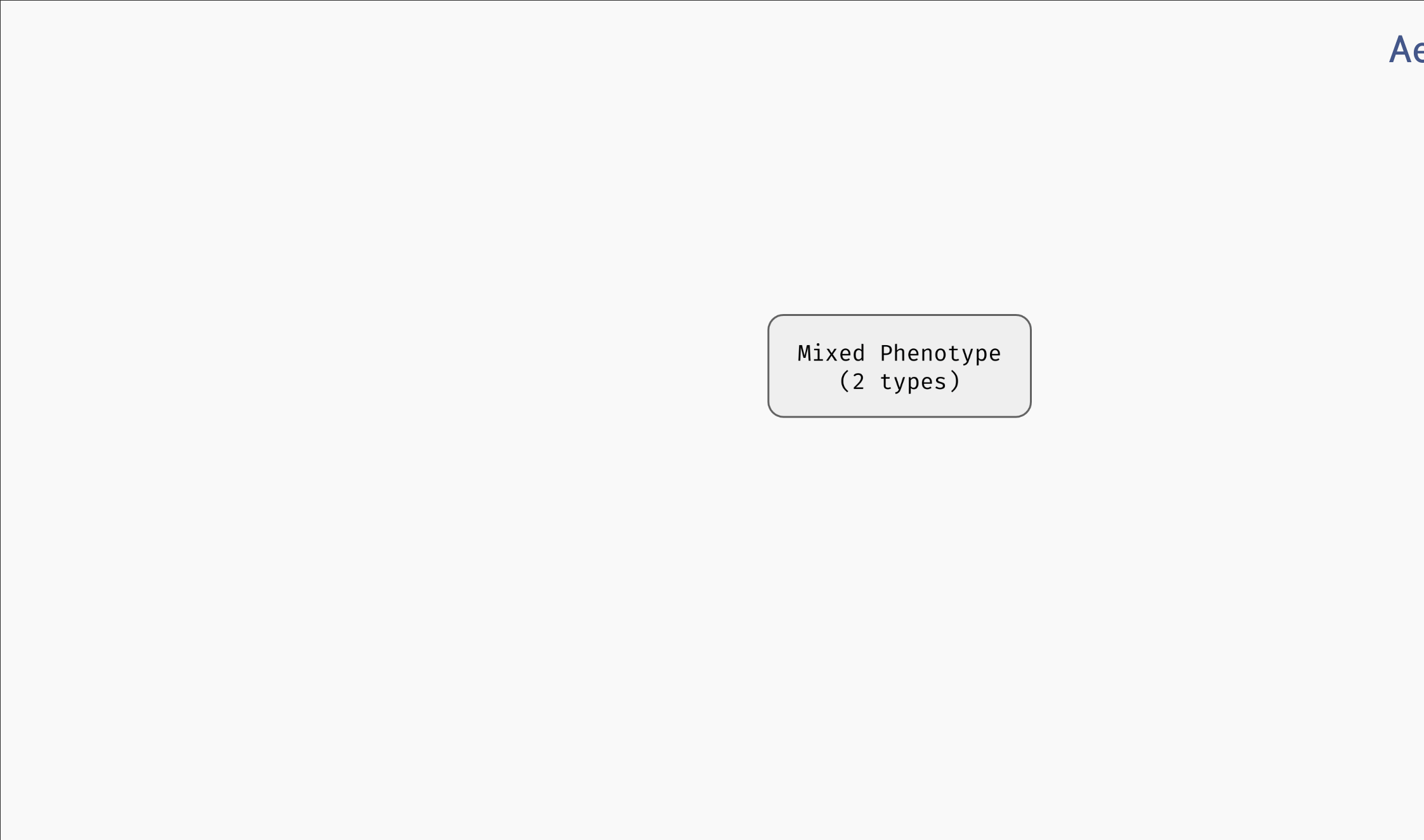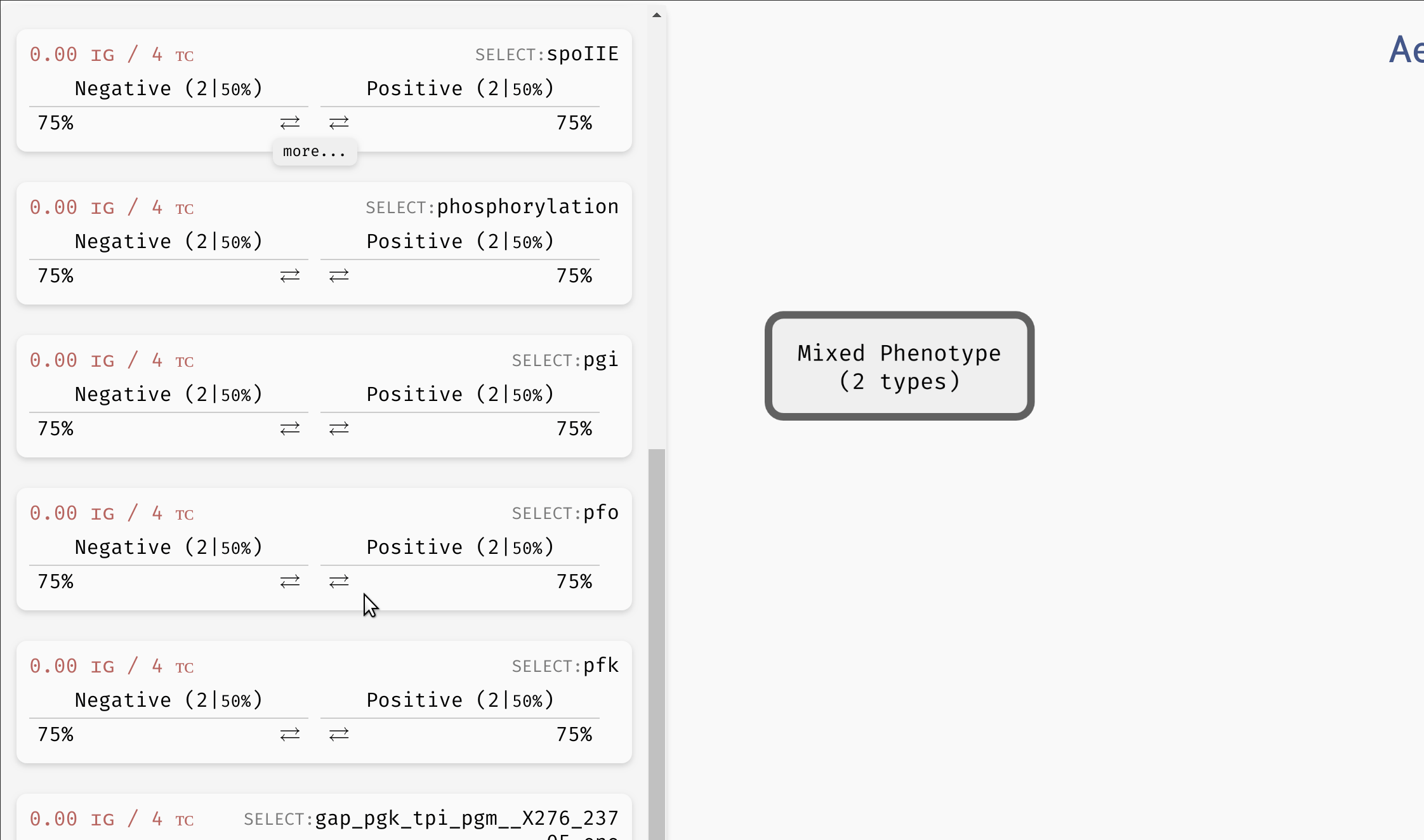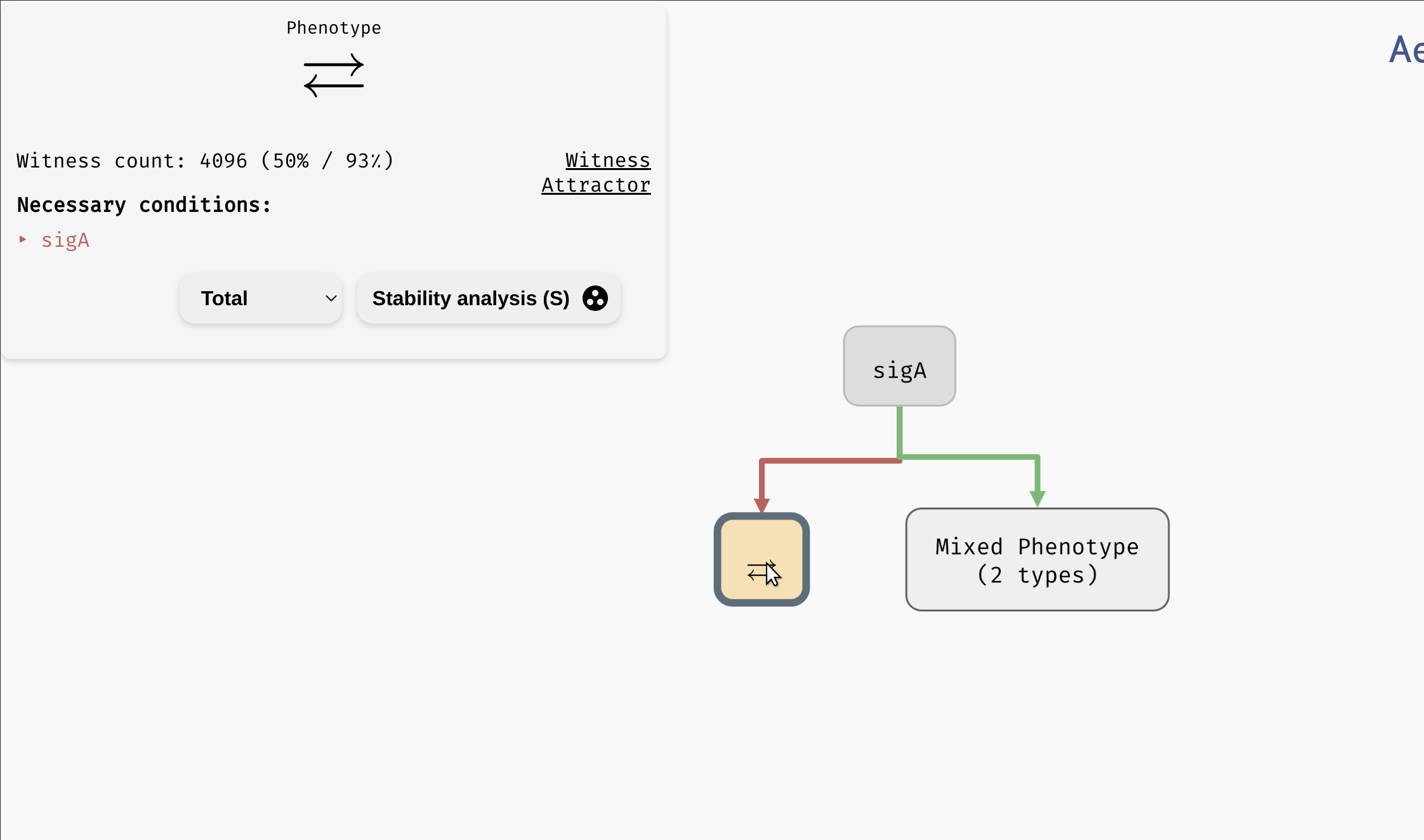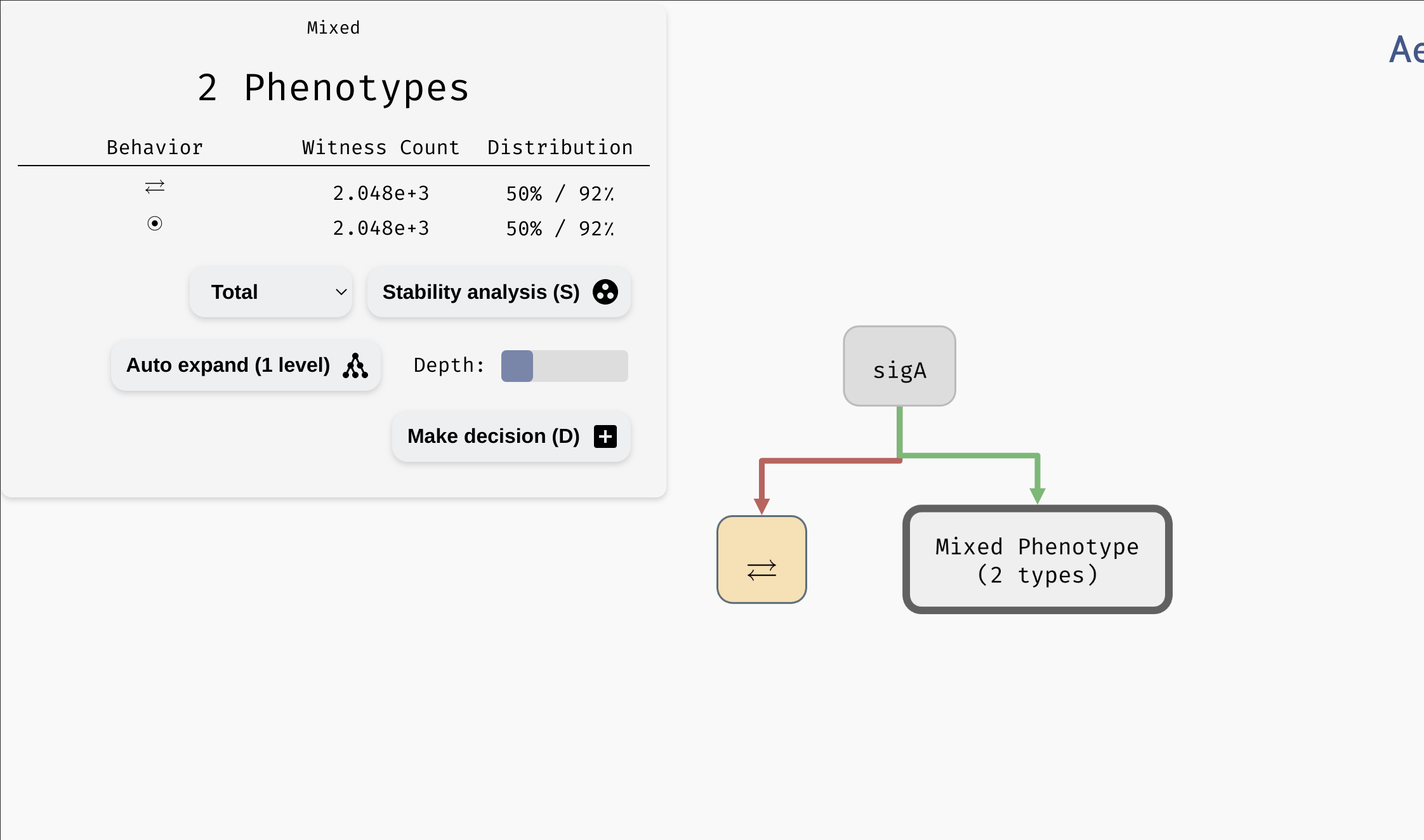Creating decision nodes. Here, a parameter sigA is selected as the decision attribute, creating one leaf node with only disordered attractors, and one mixed node.

AEON will automatically sort the attributes based on how likely it is that they lead to a concise decision tree. We use information gain as the primary sorting criterion. However, you can also pick from other sorting heuristics:

• Total number of behaviour classes in both branches after making the decision.
• Number of parametrisations in the positive or negative branch.
• Number of parametrisations in the largest class (majority) of the positive/negative branch.
• Alphabetical sort.

There is generally no "best" decision attribute. The attribute you select usually depends on what you are trying to achieve with your decision tree. On the one hand, if you already have experimental data that you are trying to reproduce, you may be restricted to a set of measured/controllable parameters. On the other hand, if you are trying to explain the presence of a particular behaviour class, you may want to minimise the number of decisions necessary to isolate said class. And so on.

In our case, AEON will suggest glucose as the next decision attribute, producing the following tree:

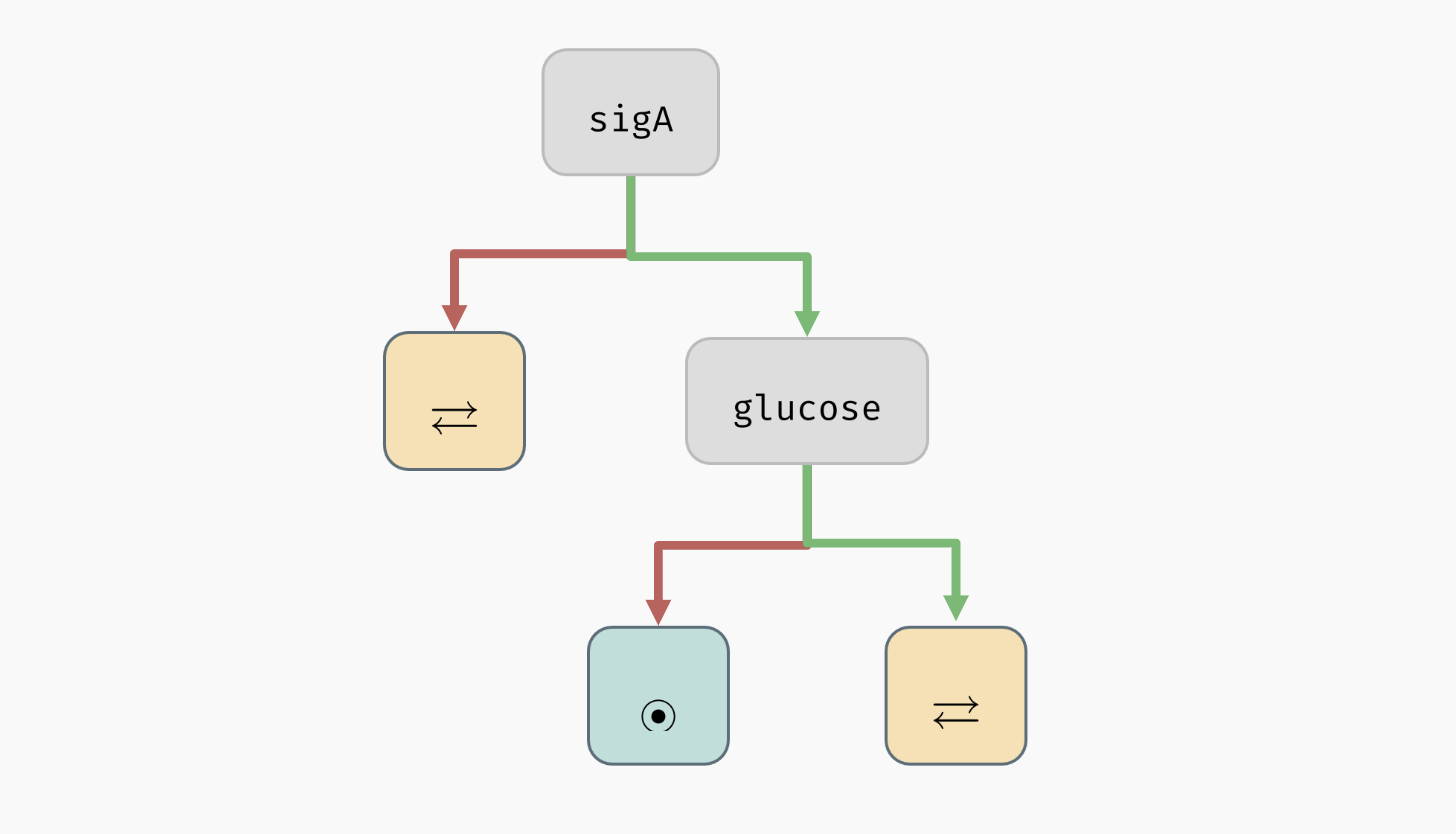A decision tree for the example model.

As you can see, all mixed nodes are now gone. This is interesting, because as you may recall, the network has 13 parameters in total. However, only two of these parameters seem to actually play a role in the type of attractors appearing in the network (the remaining parameters can still determine what specific values the network variables take in the attractors -- we will explore this in the section about stability analysis). Furthermore, we can also clearly see that to bring the network into a stable state, it is sufficient to set sigA=true and glucose=false.

If you want to, you can now delete the decision nodes (select a node and click a red X in its corner) and try a different combination of decision attributes. You should discover that for this particular model, the remaining parameters indeed play no role in determining the attractor types: you will eventually have to make decisions on sigA and glucose in either case.

You can also generate a Witness network and explore Attractor state space for each leaf node of the tree, just as you could in the overview table of the bifurcation function. Furthermore, you can ask AEON to automatically expand a mixed node up to a certain depth using the Auto Expand function (AEON will use information gain to select the decision attributes).

Decision attributes of unknown Boolean functions

As you may have noticed, up to this point, the parameters of the network were always constants that can be either true or false, so it was simple to make decision nodes. If a network contains an uninterpreted function as a parameter (for example, recall the C | f(A, B) we used in the section about parametrised networks), it is not very clear how such a function can appear in a decision tree.

One option is to simply decide based on specific values in the function table. For example, f(0,1) could be a decision attribute that fixes the value of f(0,1) to be either true or false. However, it is often very hard to understand how a decision tree with such attributes translates to real life conditions. Specifically, if we want to test such condition in the real world, we would have to ensure that both inputs of the function are fixed to a specific value, which may not be always possible.

We thus also admit a different type of decision attributes for these parameters. We say that an input X is essential in function f if the value of f depends on the value of X (recall the observability property in regulatory graphs). We can then generalize this property further, and say that X is essential in f when Y=true. This means that not only f has to depend on the value of X, it has to depend on it when Y=true.

This kind of property should be easier to test and understand, because (a) we are only fixing a partial context (Y=true) for the function, instead of the entire input vector, and (b) we are clearly stating a variable (X) that is significant in determining the resulting value of the function in that context.

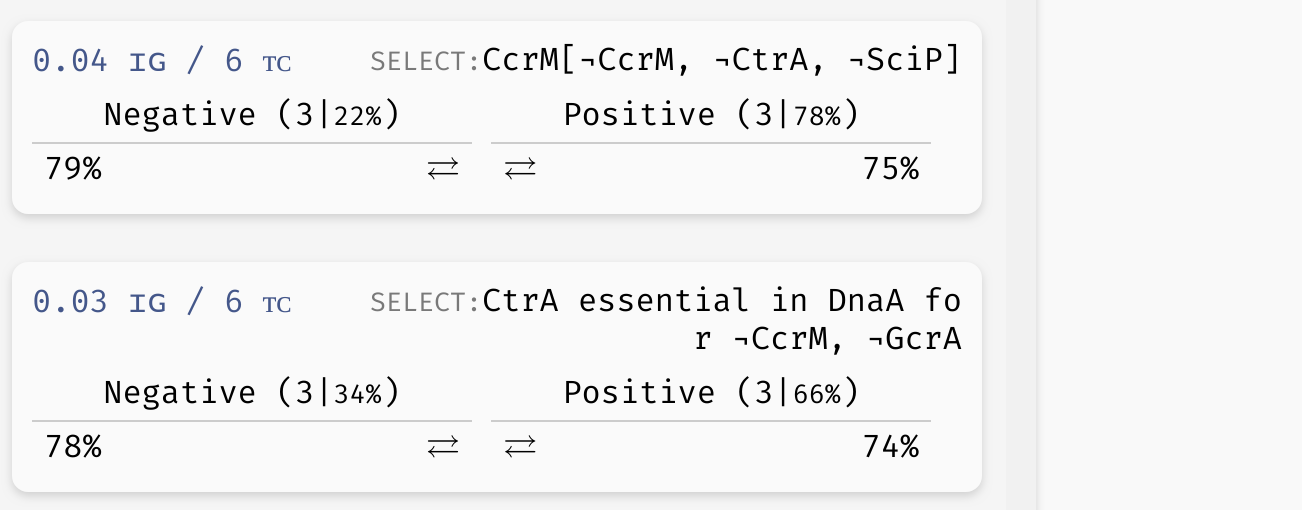Example of a basic uninterpreted function constraint (implicitly parametrised function of variable CcrM is true for CcrM=CtrA=SciP=false), as well as an essentiality constraint (variable CtrA influences the outcome of the implicit function of DnaA when CcrM=GcrA=false).

To see these attributes in action, you can explore the decision tree of the model which we will now use to discuss trees with reduced precision...

Reduced precision trees

In some cases, the decision tree is not very concise and can be hard to read. For example, let's consider another version of the G2A model available here. This model is highly parametrised (in a rather unrealistic way nonetheless), and as a result, its bifurcation decision tree is quite large. However, in a lot of its nodes, there is a distinctive majority behaviour class that appears significantly more often than other classes.

In practice, we may want to allow a node with such a class to be regarded as a leaf, thus eliminating the remaining edge cases from the tree. In the bottom right corner of the AEON interface, you should see a Precision slider. By adjusting this slider, you specify what percentage of parametrisations needs to fall into a single class for a node to be accepted as a leaf. By default, this is set to the "exact" precision of 100%, however, you can reduce the number to collapse less likely branches of the tree into leaves:

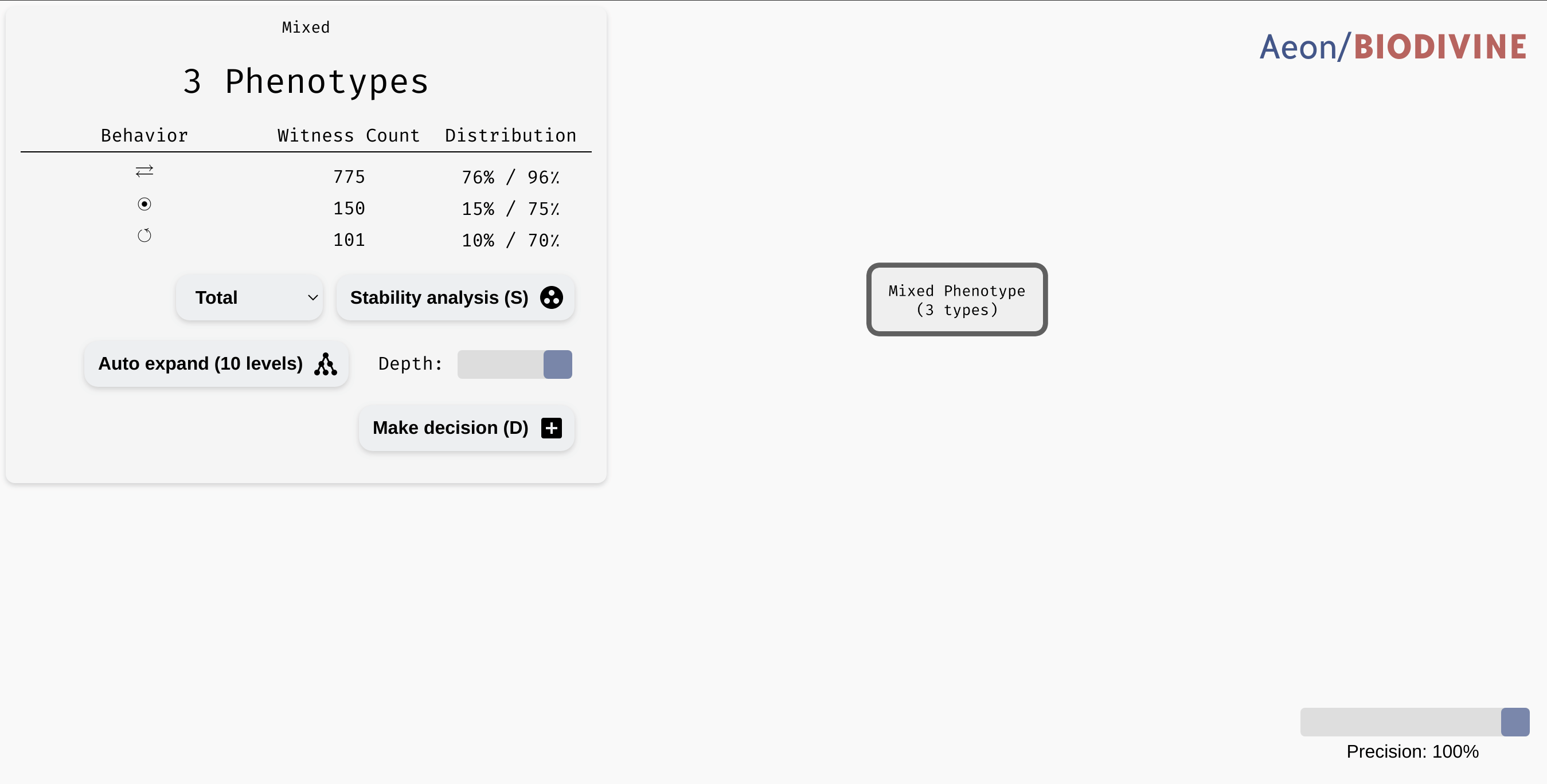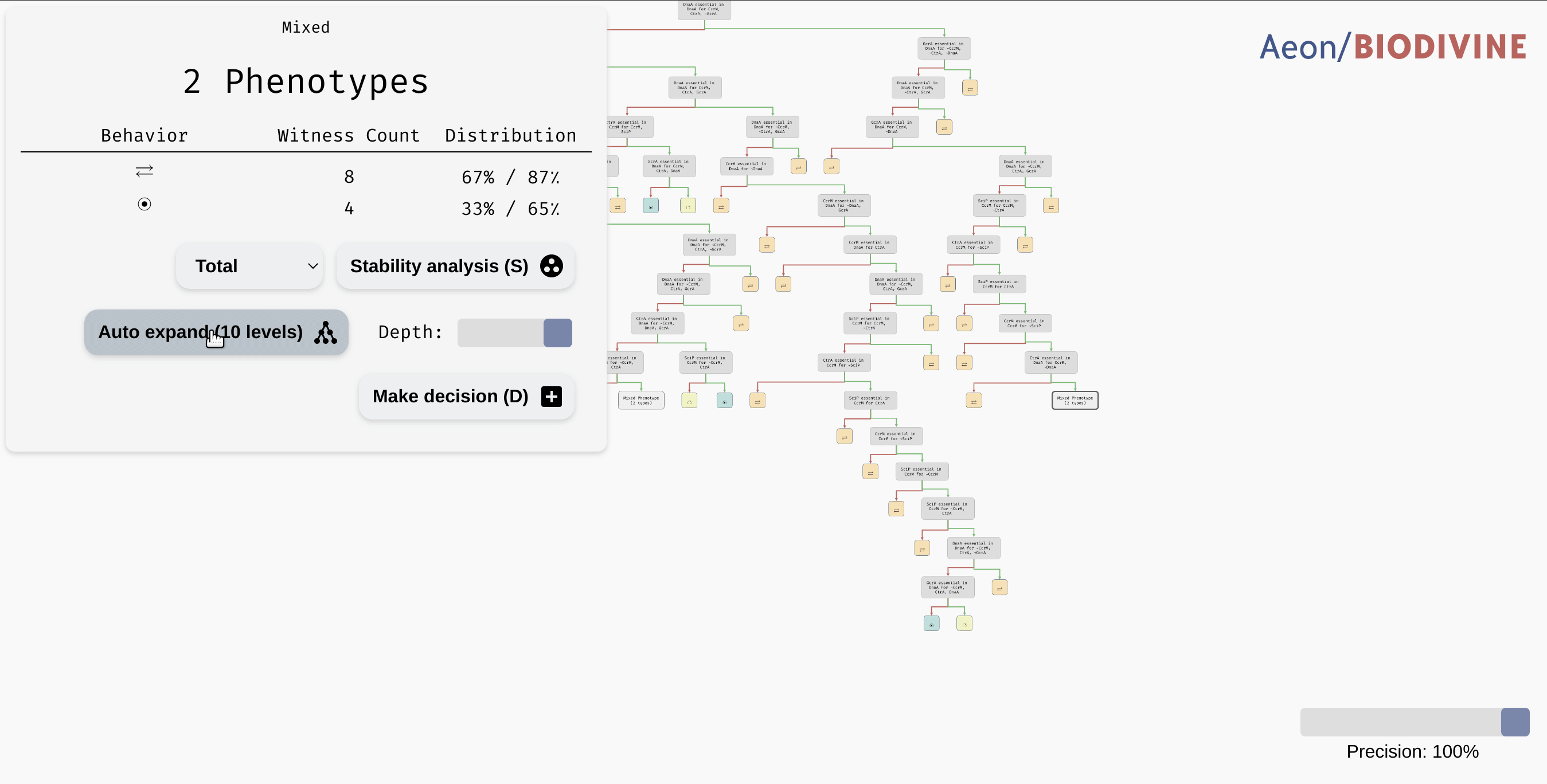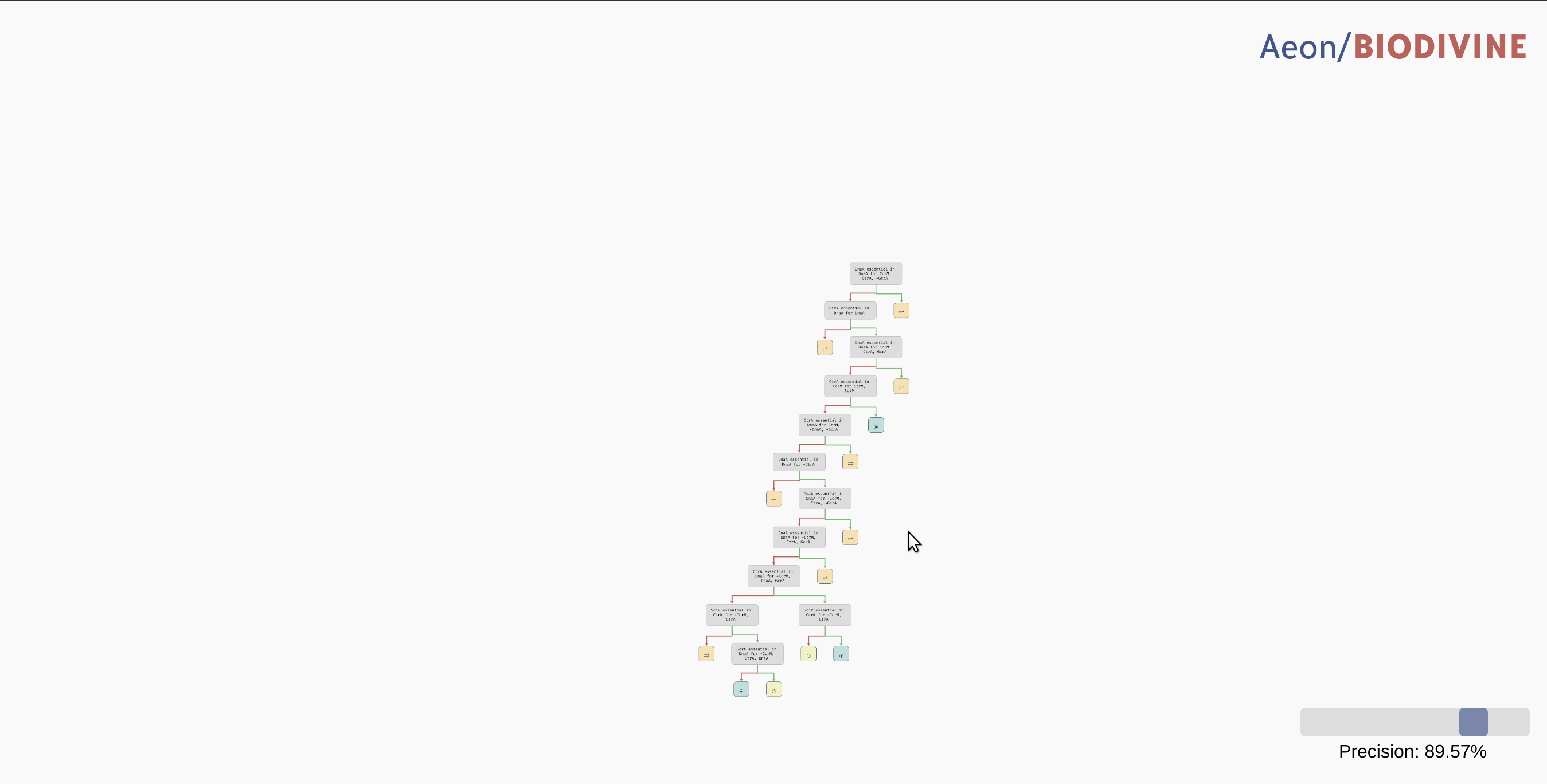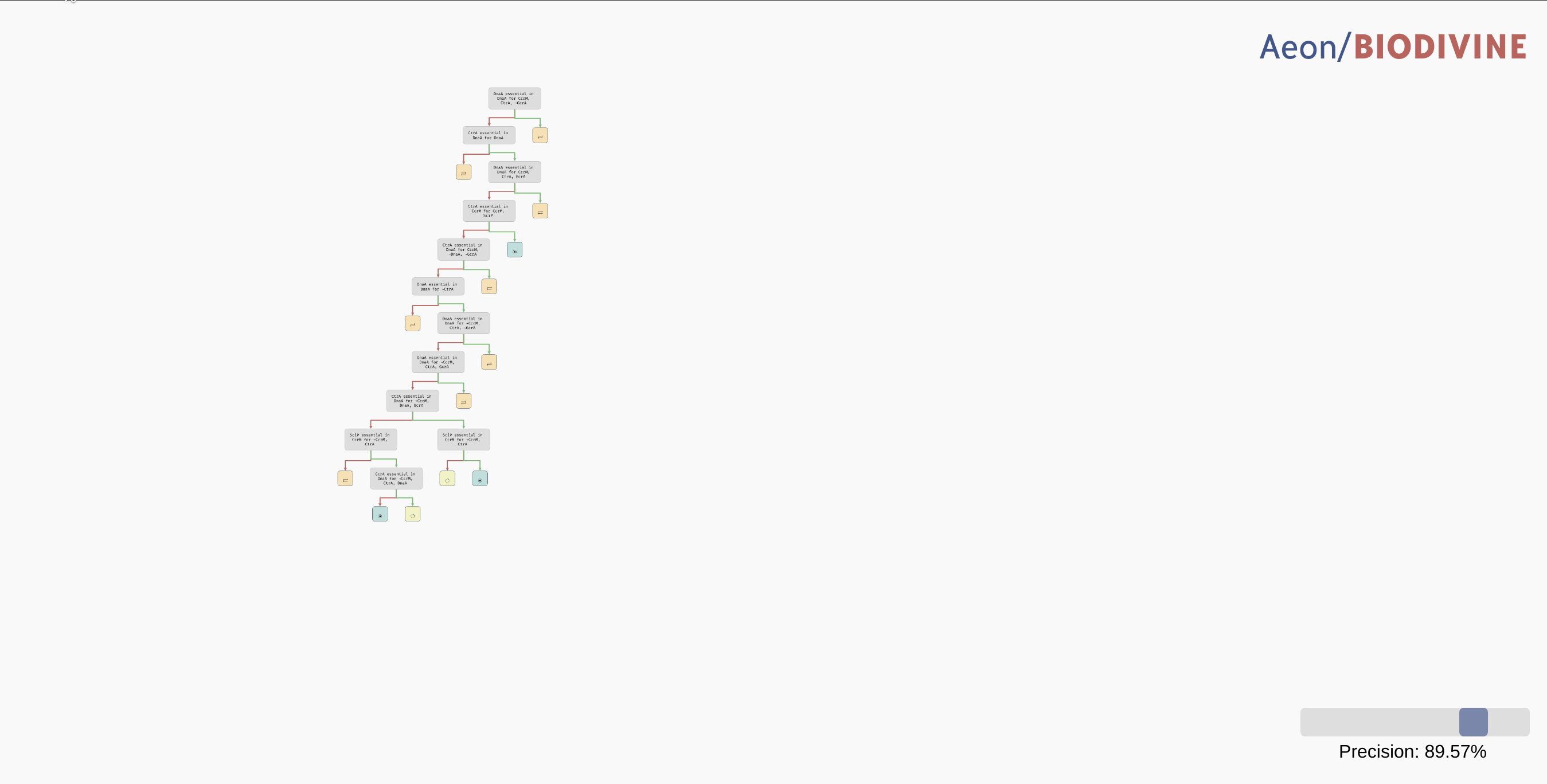Collapsing branches of a complex tree with more than 90% majority behaviour class into leaves.

In a highly parametrised model, this is a great tool for focusing only on the most statistically significant types of behaviour.

Stability analysis

In many real world situations, what we are truly interested in is not only the type of attractor (stability, oscillation, disorder), but also the values of some significant variables in that attractor. In particular, in an attractor, a variable can be stable (always true, or always false) or unstable (changing its value depending on the attractor state). Recall that in the section about state space visualisation, we saw a disordered attractor with three unstable variables (v_1, v_2, and v_4), and one stable variable (v_3). In the presence of multiple attractors, we also say that a variable may exhibit switched behaviour if there are multiple attractors such that the stability properties of the variable change from attractor to attractor.

All these properties can change with respect to parameters, but don't alter the attractor type. To analyse these types of situations, AEON contains a Stability Analysis functionality which can further divide the parameter space based on the stability of individual variables.

You can run stability analysis for any node of the bifurcation decision tree (even mixed or decision nodes). This way, you can quickly assess how the stability of variables changes in your tree. Furthermore, you can also restrict the analysis based on the attractor type to only show how the variables change in these particular attractors. Finally, for each case, you can generate a Witness network as well as visualise the Attractor state space.

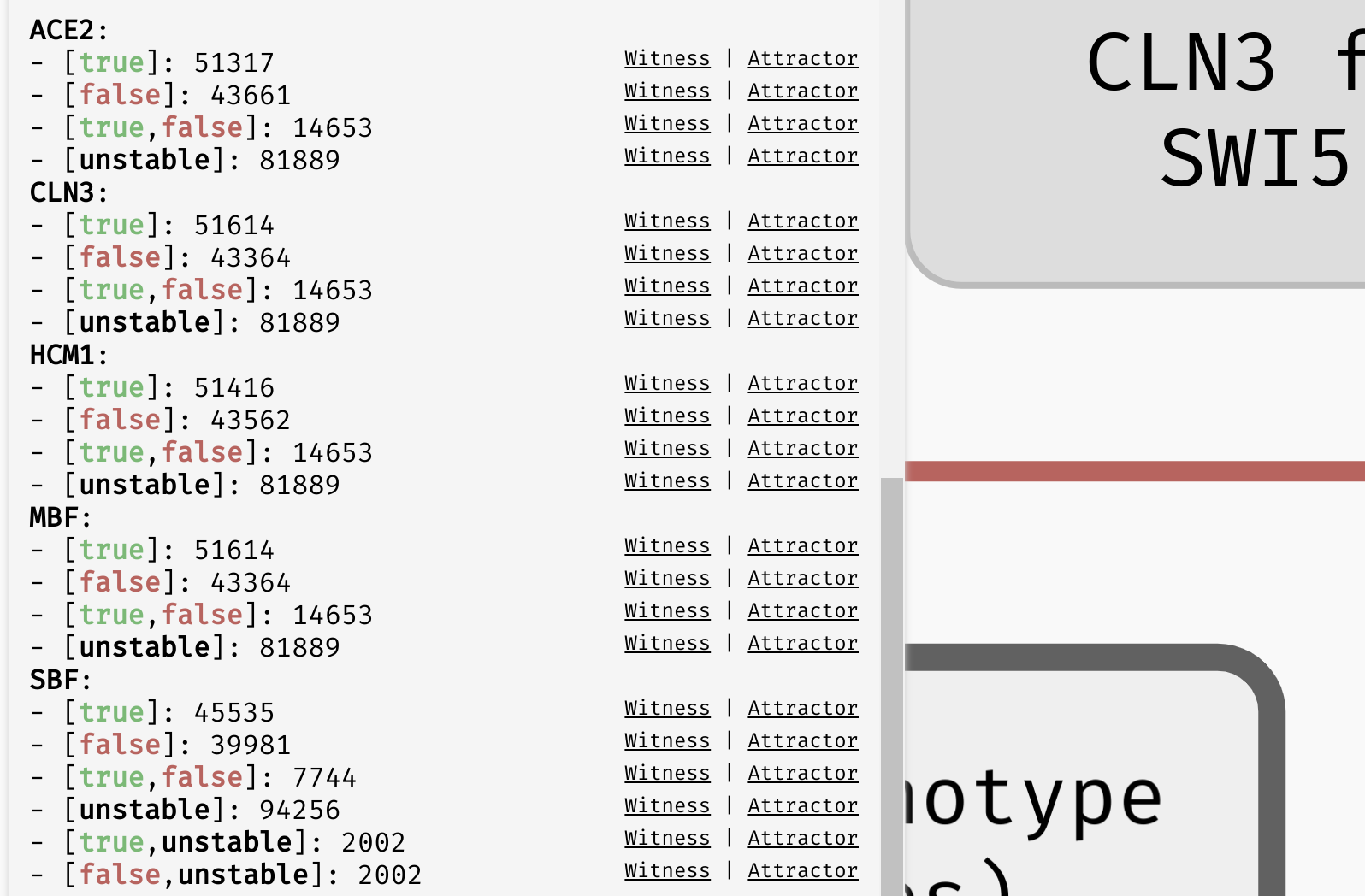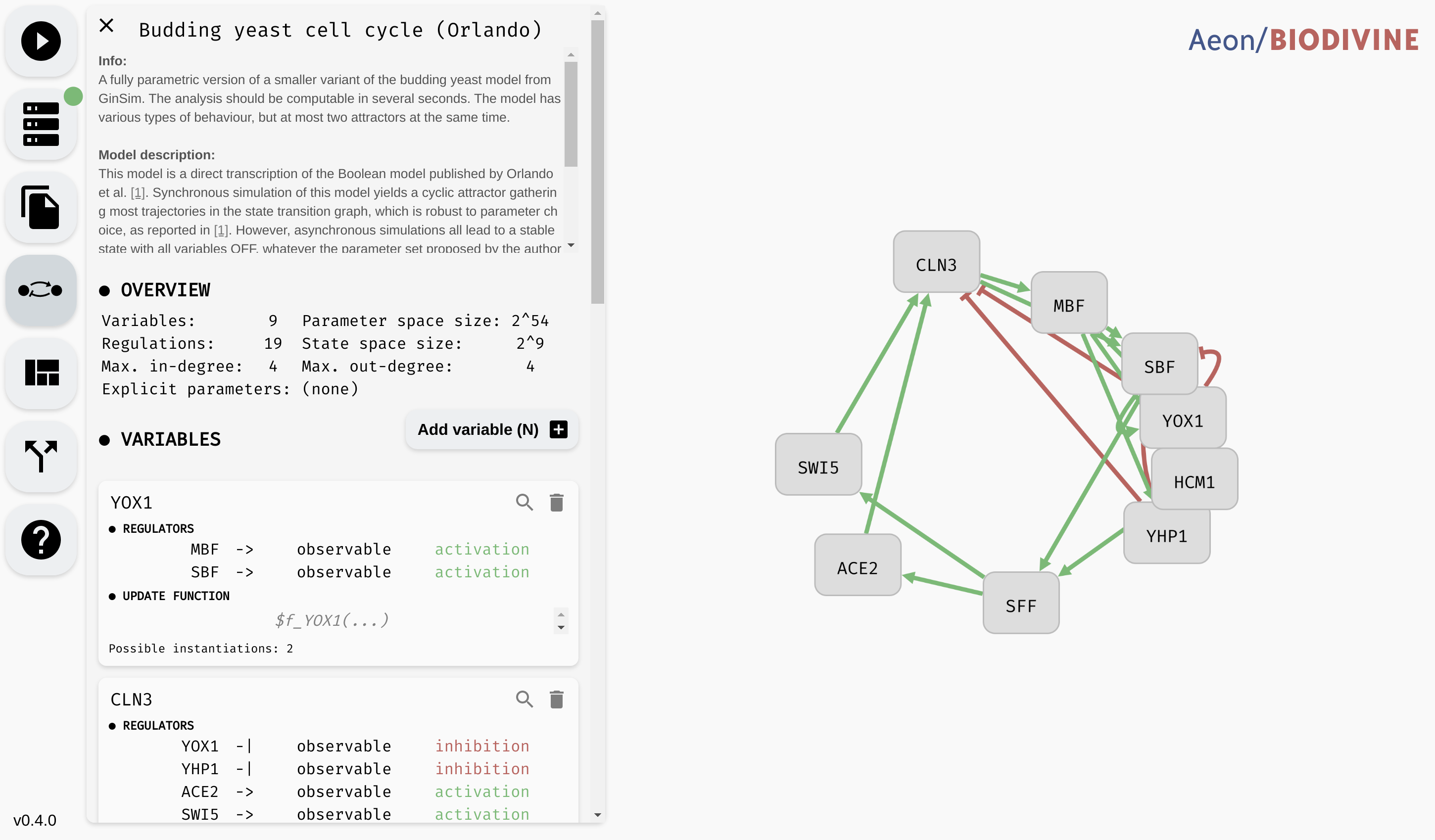
Stability analysis result for the Orlando example model. [true]/[false]/[unstable] represent situations where the variable always exhibits one type of behaviour, while multiple values (e.g. [true,false] or [true,unstable]) represent a switching behaviour.

Building Aeon

AEON lives in two Github repositories and is available under a permissive MIT license. First repository manages the web frontend, and the second one is responsible for the compute engine.

Deploying the web frontend

If you want to run your own version of the AEON frontend, you simply need to download the latest source files from the aeon-client repository (or download the sources for a particular release based on its tag). Then, you can either open the index.html file in your favourite browser, or deploy the whole directory to any webserver that is able to serve static content.

Compiling the compute engine

To run your own version of the compute engine, you need to download the source files from the aeon-server repository (again, you can either download the latest version from the master branch, or sources for a specific version based on its tag). To run or compile the compute engine, you will need the Rust nightly compiler. We recommend following the installation instructions on rust-lang.org. These will install the whole distribution into your local ~/.cargo folder, hence they do not require any elevated privileges (as opposed to some OS package managers).

Once you have completed the setup process, you need to switch from stable to the nightly compiler by executing:

rustup default nightly

Once you have the compiler ready, you can navigate to the source files you downloaded from Github, and execute

cargo run --release

to immediately compile and start the compute engine. Alternatively, you can also run

cargo build --release

which will generate the compute engine binary in ./target/release/biodivine-aeon-server.

Building this manual

This manual is available in the aeon-server repository in the manual directory, and is managed using the mdBook tool. You can follow the instructions on their website to install mdbook. Once you have mdbook ready, you simply need to navigate to the manual folder and run mdbook build to write the output files into the book directory (from here, you can deploy them as a static website). Alternatively, you can run mdbook serve to open a local webserver at http://localhost:3000 which serves the manual from your machine and automatically updates when you change its contents.